题目内容
11．
如图，以△ABC的三边为边向外作正方形，其面积分别为S1，S2，S3，且S1=9，S3=25，当S2=16时∠ACB=90°．
分析 先设Rt△ABC的三边分别为a、b、c，再分别用a、b、c表示S1、S2、S3的值，由勾股定理即可得出S2的值．
解答 解：设Rt△ABC的三边分别为a、b、c，
∴S1=a2=9，S2=b2，S3=c2=25，
∵△ABC是直角三角形，
∴a2+b2=c2，即S1+S2=S3，
∴S2=S3-S1=16．
故答案为：16．
点评 本题考查的是勾股定理的应用及正方形的面积公式，熟知勾股定理是解答此题的关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19．
下列基本图形经过平移，旋转成轴对称变换后不能得到下图的是（ ）
下列基本图形经过平移，旋转成轴对称变换后不能得到下图的是（ ）| A． | + | B． | +++ | C． |  | D． |  |
6．下列二次根式是最简二次根式的是（ ）
| A． | $\sqrt{\frac{1}{2}}$ | B． | $\sqrt{0.2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{8}$ |
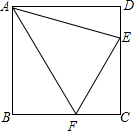如图，点E、F分别在正方形ABCD的边CD与BC上，∠EAF=45°．
3．
如图，AB⊥CD于点O，直线EF过点O，若∠AOE=65°，则∠DOF度数为（ ）
如图，AB⊥CD于点O，直线EF过点O，若∠AOE=65°，则∠DOF度数为（ ）| A． | 35° | B． | 25° | C． | 15° | D． | 10° |
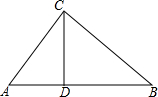△ABC中，AB=17，AC=10，AB边上的高CD=8，求BC的长．