题目内容
20．
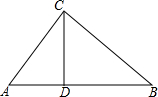△ABC中，AB=17，AC=10，AB边上的高CD=8，求BC的长．
分析 由三角形的高得出直角三角形，先根据勾股定理求出AD，得出BD，再根据勾股定理求出BC即可．
解答 解：∵CD是AB边上的高，
∴∠ADC=∠BDC=90°，
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴BD=AB-AD=17-6=11，
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{1{1}^{2}+{8}^{2}}$=$\sqrt{185}$．
点评 本题考查了勾股定理、三角形的高的性质；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
如图，以△ABC的三边为边向外作正方形，其面积分别为S1，S2，S3，且S1=9，S3=25，当S2=16时∠ACB=90°．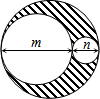
三个圆的位置如图所示，m，n分别是两个较小的圆的直径，m+n是最大的圆的直径，则图中阴影部分的面积是$\frac{π}{2}$mn．
5．长城总长约为6700010米，用科学记数法表示为（保留两位有效数字）（ ）
| A． | 6.7×105米 | B． | 6.7×106米 | C． | 6.7×107米 | D． | 6.7×108米 |
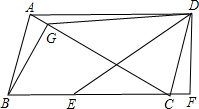在平行四边形ABCD中，CA=CB=AD，过B作BG⊥AC于G，过D作DF⊥BC于F，且BC上一点E满足DE=DG；