题目内容
9.某林业部门要考察某种幼树在一定条件下的移植成活率,在同样的条件下对这种幼树进行大量移植,并统计成活情况,记录如下(其中频率结果保留小数点后三位)| 移植总数(n) | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
| 成活数(m) | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
| 成活的频率$\frac{m}{n}$ | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
分析 对于不同批次的幼树移植成活率往往误差会比较大,为了减少误差,我们经常采用多批次计算求平均数的方法.
解答 解:$\overline{x}$=(0.800+0.940+0.870+0.923+0.883+0.890+0.915+0.905+0.902)÷9=0.892,
∴这种幼树移植成活率的概率约为0.892.
故本题答案为:0.892.
点评 此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.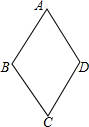 如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )
如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )
 如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )
如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )| A. | 52cm | B. | 40cm | C. | 39cm | D. | 26cm |
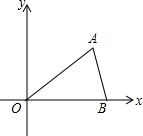 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.
 如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.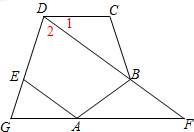 (1)计算:(2012-2016)0+$\root{3}{-8}$-(-$\frac{1}{3}$)-2.
(1)计算:(2012-2016)0+$\root{3}{-8}$-(-$\frac{1}{3}$)-2.