题目内容
11.已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$,则$\frac{a+c}{b+d}$=$\frac{2}{3}$,$\frac{a+2c-2}{b+2d-3}$=$\frac{2}{3}$.分析 分别设a为2m,c=2n,进而得到用m,n表示的b,d的值,把它们代入所给代数式求解即可.
解答 解:设a为2m,c=2n,则b=3m,d=3n.
∴$\frac{a+c}{b+d}$=$\frac{2m+2n}{3m+3n}$=$\frac{2(m+n)}{3(m+n)}$=$\frac{2}{3}$,$\frac{a+2c-2}{b+2d-3}$=$\frac{2m+2×2n-2}{3m+2×3n-3}$=$\frac{2(m+2n-1)}{3(m+2n-1)}$=$\frac{2}{3}$,
故答案为$\frac{2}{3}$,$\frac{2}{3}$.
点评 本题考查了比例的性质-等比性质的应用,若$\frac{a}{b}$=$\frac{c}{d}$=k,则$\frac{a+c}{b+d}$=k,熟练掌握比例的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.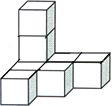 如图是由8个小正方体组合而成的几何体,它的俯视图是( )
如图是由8个小正方体组合而成的几何体,它的俯视图是( )
 如图是由8个小正方体组合而成的几何体,它的俯视图是( )
如图是由8个小正方体组合而成的几何体,它的俯视图是( )| A. | 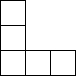 | B. | 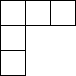 | C. |  | D. | 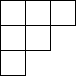 |