题目内容
4.已知关于x的方程:x2+2$\sqrt{2}$x+k=0有两个不相等的实数根x1,x2.(1)求实数k的取值范围;
(2)若$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$=-10,求k的值.
分析 (1)根据方程有两个不相等的实数根得到△>0,列出k的不等式,求出k的取值范围;
(2)根据根与系数的关系求出x1+x2=-2$\sqrt{2}$,x1x2=k,进而得到k的值.
解答 解:(1)∵方程有两个不相等的实数根,
∴△>0,
即${(2\sqrt{2})^2}-4k>0$,
∴k<2.
(2)由根与系数关系有:${x_1}+{x_2}=-2\sqrt{2}$,x1•x2=k.
∵$\frac{x_1}{x_2}+\frac{x_2}{x_1}=-10$,
∴${x_1}^2+{x_2}^2=-10{x_1}{x_2}$,
∴${({x_1}+{x_2})^2}=-8{x_1}{x_2}$,
∴${(-2\sqrt{2})^2}=-8k$,
∴k=-1.
点评 本题主要考查了根的判别式以及根与系数的关系的知识,解答本题的关键是掌握一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根以及要掌握根与系数之间的关系,此题难度一般.

练习册系列答案
相关题目
12.点P(-2,4)关于坐标原点对称的点的坐标为( )
| A. | (4,-2) | B. | (-4,2) | C. | (2,4) | D. | (2,-4) |
16.下列实数:$\frac{π}{3}$,$\frac{22}{7}$,0.414,$\root{3}{9}$,$\sqrt{36}$,$\sqrt{2}$,2.12112111211112…(相邻两个2之间依次多1),其中无理数个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.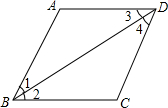 下列条件中,能说明AD∥BC的条件有( )个
下列条件中,能说明AD∥BC的条件有( )个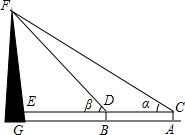 如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).