题目内容
11. 如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BD=BC,求∠ABC的度数.
如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BD=BC,求∠ABC的度数.
分析 由等腰三角形的性质和平行线的性质得出∠CBD=∠ABD.由等腰梯形的性质得出∠BCD=∠ABC=2∠CBD.再由等腰三角形的性质得出∠BDC=∠BCD.设∠CBD=x,则∠BDC=∠BCD=2x.在△BCD中,由三角形内角和定理得出方程,解方程求出x,即可得出∠ABC的度数.
解答 解:∵AB=AD,
∴∠ABD=∠ADB.
∵AD∥BC,
∴∠CBD=∠ADB.
∴∠CBD=∠ABD.
∵在梯形ABCD中,AD∥BC,AB=CD,
∴∠BCD=∠ABC=2∠CBD.
∵BD=BC,
∴∠BDC=∠BCD.
设∠CBD=x,则∠BDC=∠BCD=2x.
在△BCD中,∠CBD+∠CDB+∠BCD=180°,
即x+2x+2x=180°,
解得:x=36°.
∴∠ABC=72°
点评 本题考查了等腰梯形的性质、等腰三角形的性质、平行线的性质、三角形内角和定理;熟练掌握等腰梯形的性质,由角的关系和三角形内角和定理得出方程是解决问题的关键.

练习册系列答案
相关题目
19.下列说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 0表示没有 | ||
| C. | 一个有理数不是整数就是分数 | D. | 正数和0的绝对值是本身 |
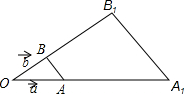 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)? 如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.
如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.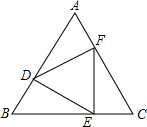 如图,在等边△ABC的三边上分别取点D、E、F,使AD=BE=CF.
如图,在等边△ABC的三边上分别取点D、E、F,使AD=BE=CF. 在美化校园的活动中,某数学兴趣小组的同学利用长为16m的篱笆,借助两面互相垂直的墙体a、b围一个矩形花圃ABCD(墙体a,b的最大可用长度为14m、9m),设花圃AB边的长为x m,面积为S m2
在美化校园的活动中,某数学兴趣小组的同学利用长为16m的篱笆,借助两面互相垂直的墙体a、b围一个矩形花圃ABCD(墙体a,b的最大可用长度为14m、9m),设花圃AB边的长为x m,面积为S m2 某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形图.那么喜爱跳绳的学生有30人.
某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形图.那么喜爱跳绳的学生有30人.