题目内容
2.已知一元二次方程x2-3x+1=0的两根为a、b.求下列代数式的值:(1)$\frac{b}{a}+\frac{a}{b}$
(2)|a-b|
(3)a+3b.
分析 根据根与系数的关系得出a+b=3,ab=1,进一步整理:
(1)$\frac{b}{a}+\frac{a}{b}$=$\frac{(a+b)^{2}-2ab}{ab}$;
(2)|a-b|=$\sqrt{(a+b)^{2}-2ab}$;
(3)由(2)得出a-b,求得2b,a+3b=a+b+2b.整体代入求出即可.
解答 解:∵一元二次方程x2-3x+1=0的两根为a、b,
∴a+b=3,ab=1;
(1)$\frac{b}{a}+\frac{a}{b}$=$\frac{(a+b)^{2}-2ab}{ab}$=7;
(2)|a-b|=$\sqrt{(a+b)^{2}-2ab}$=$\sqrt{7}$;
(3)a-b=±$\sqrt{7}$,a+b=3,
2b=3+$\sqrt{7}$或3-$\sqrt{7}$,
a+3b=6+$\sqrt{7}$或6-$\sqrt{7}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
 如图所示,有一抛物线形拱桥,当水位线在AB位置时,拱桥离水面2m,水面宽4m,水面下降1m后,求水面的宽.
如图所示,有一抛物线形拱桥,当水位线在AB位置时,拱桥离水面2m,水面宽4m,水面下降1m后,求水面的宽. 已知△ABC中,BC=26cm,AB、AC的垂直平分线分别交BC于E、F,则△EAF周长26cm.
已知△ABC中,BC=26cm,AB、AC的垂直平分线分别交BC于E、F,则△EAF周长26cm.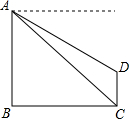 小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°.
小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°. 如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BD=BC,求∠ABC的度数.
如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BD=BC,求∠ABC的度数. 已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题.
已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题.