题目内容
1.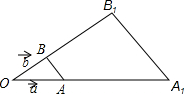 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?
分析 由$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,利用三角形法则,可求得$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$;即可得$\overrightarrow{{A}_{1}{B}_{1}}$=3$\overrightarrow{AB}$,结合图形,即可判定$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$平行.
解答 解:∵$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,
∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=$\overrightarrow{b}$-$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{O{B}_{1}}$-$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$;
$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$平行.
理由:∵$\overrightarrow{{A}_{1}{B}_{1}}$=3($\overrightarrow{b}$-$\overrightarrow{a}$)=3$\overrightarrow{AB}$,
∴$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$平行.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用,注意理解平行向量的定义.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| 日 期 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 | 21日 | 22日 |
| 天然气表显示的读数/m3 | 220 | 229 | 241 | 249 | 259 | 270 | 279 | 290 |
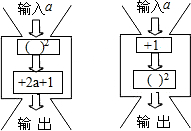 分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?
分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律? 如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BD=BC,求∠ABC的度数.
如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BD=BC,求∠ABC的度数.