题目内容
2.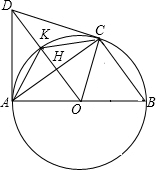 AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.
AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.
分析 由CD与⊙O相切于点C可得出∠OCD=90°,结合DA⊥AB即可得出∠OAD=90°=∠OCD,再由公共边OD即可通过全等三角形的判定定理HL证得两直角三角形△OAD≌△OCD,由此得出∠AOD=∠COD,即得出OD⊥AC.在Rt△OCD中,∠OCD=90°,OC=3,DC=4,由勾股定理及∠COD的正余弦值,可得出OD、CH、OH的长度,由OK=OH+HK即可得出HK的长度,结合OD=OK+DK可得出DK的长度,最后再在Rt△CHK和Rt△ACB中由勾股定理算出CK与BC的长.
解答 解:∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵DA⊥AB,
∴∠OAD=90°=∠OCD,
在Rt△OAD和Rt△OCD中,有$\left\{\begin{array}{l}{OA=OC}\\{OD=OD}\end{array}\right.$,
∴△OAD≌△OCD(HL).
∴∠AOD=∠COD.
又∵OA=OC,
∴OD⊥AC.
在Rt△OCD中,∠OCD=90°,OC=3,DC=4,
∴OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=5,
∴sin∠COD=$\frac{CD}{OD}$=$\frac{4}{5}$,cos∠COD=$\frac{OC}{OD}$=$\frac{3}{5}$,
∴CH=OC•sin∠COD=3×$\frac{4}{5}$=$\frac{12}{5}$,OH=OC•cos∠COD=3×$\frac{3}{5}$=$\frac{9}{5}$,HK=OK-OH=3-$\frac{9}{5}$=$\frac{6}{5}$,DK=OD-OK=5-3=2.
在Rt△CHK中,∠CHK=90°,CH=$\frac{12}{5}$,HK=$\frac{6}{5}$,
∴CK=$\sqrt{H{K}^{2}+C{H}^{2}}$=$\frac{6\sqrt{5}}{5}$.
∵AB为直径,
∴∠ACB=90°.
在Rt△ACB中,∠ACB=90°,AC=2CH=$\frac{24}{5}$,AB=2OA=6,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\frac{18}{5}$.
点评 本题考查了切线的性质、勾股定理、解直角三角形以及全等三角形的判定及性质,解题的关键是找出OD⊥AC,在各直角三角形中解决边的长度.本题属于中档题,难度不大,但该问中要求6条线段的长度,易造成混淆,解决该题型题目时,由边角关系结合勾股定理算出边长是关键.

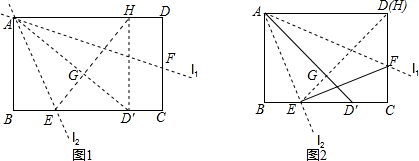
 由5个相同的小正方体组成的几何体如图所示,这个几何体的主视图是( )
由5个相同的小正方体组成的几何体如图所示,这个几何体的主视图是( )



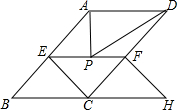 如图,在?ABCD中,AB=7,BC=5,sinB=$\frac{4}{5}$,将?ABCD折叠,使点A落在点C上,点D的对应点为H,折痕为EF.
如图,在?ABCD中,AB=7,BC=5,sinB=$\frac{4}{5}$,将?ABCD折叠,使点A落在点C上,点D的对应点为H,折痕为EF.