题目内容
5. 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2$\sqrt{2}$,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F
如图,在四边形ABCD中,AD∥BC,AD=2,AB=2$\sqrt{2}$,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F(1)求∠ABE的大小及$\widehat{DEF}$的长度;
(2)在BE的延长线上取一点G,使得$\widehat{DE}$上的一个动点P到点G的最短距离为2$\sqrt{2}$-2,求BG的长.
分析 (1)连接AE,如图1,根据圆的切线的性质可得AE⊥BC,解Rt△AEB可求出∠ABE,进而得到∠DAB,然后运用圆弧长公式就可求出$\widehat{DEF}$的长度;
(2)如图2,根据两点之间线段最短可得:当A、P、G三点共线时PG最短,此时AG=AP+PG=2$\sqrt{2}$=AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
解答  解:(1)连接AE,如图1,
解:(1)连接AE,如图1,
∵AD为半径的圆与BC相切于点E,
∴AE⊥BC,AE=AD=2.
在Rt△AEB中,
sin∠ABE=$\frac{AE}{AB}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴∠ABE=45°.
∵AD∥BC,
∴∠DAB+∠ABE=180°,
∴∠DAB=135°,
∴$\widehat{DEF}$的长度为$\frac{135π•2}{180}$=$\frac{3π}{2}$;
(2)如图2,
根据两点之间线段最短可得:
当A、P、G三点共线时PG最短,
此时AG=AP+PG=2+2$\sqrt{2}$-2=2$\sqrt{2}$,
∴AG=AB.
∵AE⊥BG,
∴BE=EG.
∵BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{8-4}$=2,
∴EG=2,
∴BG=4.
综上,存在满足条件的BG=4.
点评 本题主要考查了圆的切线的性质、三角函数的定义、特殊角的三角函数值、平行线的性质、圆弧长公式、等腰三角形的性质、两点之间线段最短、勾股定理等知识,根据两点之间线段最短得到A、P、G三点共线时PG最短,是解决第(2)小题的关键,注意有两解.

练习册系列答案
相关题目
15.在一个不透明的布袋中装有3个白球和5个红球,它们除了颜色不同外,其余均相同,从中随机摸出一个球,摸到红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
20.与-2的乘积为1的数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 如图,?ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.
如图,?ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.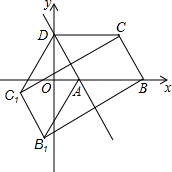 如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D
如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D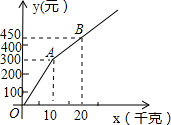 甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系. 如图,已知AD=BC,AC=BD.
如图,已知AD=BC,AC=BD.