Question

8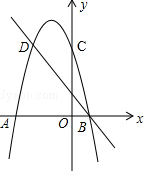．如图，二次函数y=-x²-2x+3的图象与x轴交于A和B两点（A在B左边），交y轴于点C，C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．
（1）求这个二次函数的最大值；
（2）求点A、B、C、D的坐标；
（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围．

Answer 1

分析 （1）利用公式法或配方法求出二次函数的最大值即可；
（2）设y=0，可求出点A，B的坐标；设x=0，可求出点C的坐标；利用点C、D是二次函数图象上的一对对称点，可得出D点的坐标；
（3）观察函数图象，写出一次函数图象在抛物线上方所对应的自变量的范围即可．

解答 解：
（1）∵y=-x²-2x+3=-（x+1）²+4，
∴这个二次函数的最大值是4；
（2）设y=0，则0=-x²-2x+3，
解得：x=-3或1，
∵A在B左边，
∴点A（-3，0），B（1，0），
设x=0，则y=3，
∴点C坐标（0，3），
∵抛物线的对称轴是x=-1，而C、D关于直线x=-1对称；
∴D（-2，3）；
（3）根据图象可看出B、D两点之外的函数图象是一次函数值大于二次函数值，
∴x＜-2或x＞1．

点评 本题考查了抛物线与x轴的交点：由二次函数的交点式y=a（x-x₁）（x-x₂）（a，b，c是常数，a≠0）可直接得到抛物线与x轴的交点坐标（x₁，0），（x₂，0）．也考查了二次函数与不等式的关系．