题目内容
13.化简:$\frac{2}{\sqrt{12-4\sqrt{5}}}$-$\frac{1}{\sqrt{3+\sqrt{5}}}$=$\frac{\sqrt{10}}{4}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$+2.分析 利用完全平方公式变形得到原式=$\frac{2}{\sqrt{(\sqrt{10}-\sqrt{2})^{2}}}$-$\frac{1}{\frac{\sqrt{(\sqrt{3}+\sqrt{2})^{2}}}{\sqrt{2}}}$,然后利用二次根式的性质化简后进行分母有理化即可.
解答 解:原式=$\frac{2}{\sqrt{12-2\sqrt{20}}}$-$\frac{1}{\sqrt{\frac{6+2\sqrt{5}}{2}}}$
=$\frac{2}{\sqrt{(\sqrt{10}-\sqrt{2})^{2}}}$-$\frac{1}{\frac{\sqrt{(\sqrt{3}+\sqrt{2})^{2}}}{\sqrt{2}}}$
=$\frac{2}{\sqrt{10}-\sqrt{2}}$-$\frac{\sqrt{2}}{\sqrt{3}+\sqrt{2}}$
=$\frac{\sqrt{2}}{\sqrt{5}-1}$-$\sqrt{2}$($\sqrt{3}$-$\sqrt{2}$)
=$\frac{\sqrt{10}}{4}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$+2.
故答案为$\frac{\sqrt{10}}{4}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$+2.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
5.圆柱的体积V、高h、底面圆的半径R之间的解析式是V=πR2h,已知V=50cm3,填写下表:
(1)变量h是变量R的函数吗?
(2)变量h是变量R的反比例函数吗?
| R(cm) | 1 | 2 | 3 | 4 | 5 | 6 |
| h(cm) | $\frac{50}{π}$ | $\frac{25}{2π}$ | $\frac{50}{9π}$ | $\frac{25}{8π}$ | $\frac{2}{π}$ | $\frac{25}{8π}$ |
(2)变量h是变量R的反比例函数吗?
 如图,如果AB∥CD,根据两直线平行,内错角相等可得∠1=∠BDF;根据两直线平行,同旁内角互补,可得∠1+∠BDC=180°.
如图,如果AB∥CD,根据两直线平行,内错角相等可得∠1=∠BDF;根据两直线平行,同旁内角互补,可得∠1+∠BDC=180°.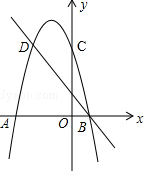 如图,二次函数y=-x2-2x+3的图象与x轴交于A和B两点(A在B左边),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数y=-x2-2x+3的图象与x轴交于A和B两点(A在B左边),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 如图,点C分线段AB为2:1两部分,D点为线段CB的中点,AD=5,求线段AB的长.
如图,点C分线段AB为2:1两部分,D点为线段CB的中点,AD=5,求线段AB的长.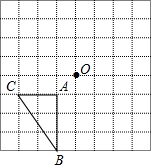 如图所示,△ABC的顶点与点O在8×8的网格中的格点上.
如图所示,△ABC的顶点与点O在8×8的网格中的格点上.