题目内容
12.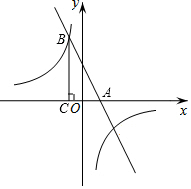 如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).
如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线y=$\frac{m}{x}$上,且△PAC的面积为4,求点P的坐标.
分析 (1)将点B(-1,4)代入直线和双曲线解析式求出k和m的值即可;
(2)根据直线解析式求得点A坐标,由${S_{△ACP}}=\frac{1}{2}AC•|{y_P}|=4$求得点P的纵坐标,继而可得答案.
解答 解:(1)∵直线y=kx+3(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)都经过点B(-1,4),
∴-k+3=4,m=-1×4.
∴k=-1,m=-4.
∴直线的表达式为y=-x+3,双曲线的表达式为$y=-\frac{4}{x}$.
(2)由题意,得点C的坐标为C(-1,0),
直线y=-x+3与x轴交于点A(3,0).
∴AC=4.
∵${S_{△ACP}}=\frac{1}{2}AC•|{y_P}|=4$,
∴yP=±2.
∵点P在双曲线$y=-\frac{4}{x}$上,
∴点P的坐标为P1(-2,2)或P2(2,-2).
点评 本题主要考查反比例函数和一次函数的交点问题,熟练掌握待定系数法求函数解析式及三角形的面积是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,BC是⊙O的直径,BC=4$\sqrt{2}$,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在$\widehat{MN}$上从点M运动到点N时,点E运动的路径长是( )
如图,BC是⊙O的直径,BC=4$\sqrt{2}$,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在$\widehat{MN}$上从点M运动到点N时,点E运动的路径长是( )
 如图,BC是⊙O的直径,BC=4$\sqrt{2}$,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在$\widehat{MN}$上从点M运动到点N时,点E运动的路径长是( )
如图,BC是⊙O的直径,BC=4$\sqrt{2}$,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在$\widehat{MN}$上从点M运动到点N时,点E运动的路径长是( )| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
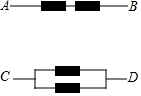 已知电流在一定时间段内正常通过电子元件的概率是0.5,用列表或画树状图的方法分别求在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率.(提示:可用1、0分别表示电子元件的通与不通两种状态)
已知电流在一定时间段内正常通过电子元件的概率是0.5,用列表或画树状图的方法分别求在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率.(提示:可用1、0分别表示电子元件的通与不通两种状态) 如图,点A、B、C在⊙O上,点B是$\widehat{AC}$的中点,∠ABC=∠AOC,将四边形AOCB绕点A按顺时针方向旋转一定角度后,点C落在圆上的点D处,连结OD.
如图,点A、B、C在⊙O上,点B是$\widehat{AC}$的中点,∠ABC=∠AOC,将四边形AOCB绕点A按顺时针方向旋转一定角度后,点C落在圆上的点D处,连结OD.
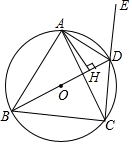 如图,BD是⊙O的直径,四边形ABCD是⊙O的内接四边形,且AB=AC,AH⊥BD于点H,延长CD至点E.
如图,BD是⊙O的直径,四边形ABCD是⊙O的内接四边形,且AB=AC,AH⊥BD于点H,延长CD至点E.