题目内容
1. 如图,BC是⊙O的直径,BC=4$\sqrt{2}$,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在$\widehat{MN}$上从点M运动到点N时,点E运动的路径长是( )
如图,BC是⊙O的直径,BC=4$\sqrt{2}$,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在$\widehat{MN}$上从点M运动到点N时,点E运动的路径长是( )| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
分析 如图,连接BE、CE,由∠BAC=90°,E是内心,推出∠BEC=135°,推出点E在以P为圆心的PC为半径的圆上运动(轨迹是$\widehat{GH}$),求出PG,∠GPH即可解决问题.
解答 解:如图,连接BE、CE,
∵∠BAC=90°,E是内心,
∴∠BEC=135°,
∴点E在以P为圆心的PC为半径的圆上运动(轨迹是$\widehat{GH}$),在⊙P上取一点M,连接BM、CM,则∠M=180°-135°=45°,∠BPC=2∠M=90°,
∴△BCP是等腰直角三角形,
∵BC=4$\sqrt{2}$,
∴PB=PC=4, ∵∠HPC=2∠HBC=∠NBC=$\frac{1}{2}$∠NOC,同理∠GPB=$\frac{1}{2}$∠MOB,
∵∠HPC=2∠HBC=∠NBC=$\frac{1}{2}$∠NOC,同理∠GPB=$\frac{1}{2}$∠MOB,
∴∠HPC+∠GPB=$\frac{1}{2}$(∠NOC+∠MOB)=30°,
∴∠GPH=60°,
∴点E运动的路径长是$\frac{60π•4}{180}$=$\frac{4}{3}$π,
故选B.
点评 本题考查三角形的内心、三角形的外接圆与外心等知识,解题的关键是正确寻找点E的运动轨迹,学会添加辅助圆解决问题,属于中考选择题中的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列8个数中:$-\root{3}{8}$,0.131131113…(相邻两个3之间依次多一个1),0,sin45°,$\sqrt{25}$,-π,$\frac{22}{7}$,$-\sqrt{27}$,无理数的个数有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
11.按照《浙江省人口发展“十三五”规划》制定的目标,“十三五”期间,我省人口发展将实现全面两孩政策生育堆积平稳过渡,生育水平适度提高,总和生育率上升到1.6左右,到2020年末,常住人口达到总量5750万人左右.5750万人用科学记数法表示正确的是( )
| A. | 5.75×103人 | B. | 5750×104人 | C. | 5.75×107人 | D. | 5.75×108人 |
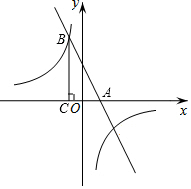 如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).
如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).