题目内容
20.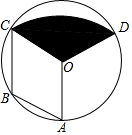 如图,点A、B、C在⊙O上,点B是$\widehat{AC}$的中点,∠ABC=∠AOC,将四边形AOCB绕点A按顺时针方向旋转一定角度后,点C落在圆上的点D处,连结OD.
如图,点A、B、C在⊙O上,点B是$\widehat{AC}$的中点,∠ABC=∠AOC,将四边形AOCB绕点A按顺时针方向旋转一定角度后,点C落在圆上的点D处,连结OD.(1)求证:四边形AOCB为菱形;
(2)若⊙O的半径为2,求图中阴影部分的面积.
分析 (1)连接半径OB,证明△AOB≌△COB(SAS),得∠CBO=∠ABO=$\frac{1}{2}$∠ABC,证明△BCO是等腰三角形,得:AB=AO=OB=OC=BC,则四边形AOCB为菱形;
(2)观察图形得:阴影部分面积=扇形CAD的面积-2个△CAO的面积,由菱形的对角线互相垂直得:AC⊥OB,与△ABO和△CBO是等边三角形,则∠OCB=∠OAB=60°,有30°存在,根据直角三角形30°的性质可知:AC和扇形的圆心角∠CAD=60°,代入扇形的面积公式可得阴影图形的面积.
解答  证明:(1)连接OB,
证明:(1)连接OB,
∵点B是$\widehat{AC}$的中点,
∴∠COB=∠AOB=$\frac{1}{2}$∠AOC,
∵OA=OB=OC,
∴△AOB≌△COB(SAS),
∴∠CBO=∠ABO=$\frac{1}{2}$∠ABC,
∵∠ABC=∠AOC,
∴∠CBO=∠COB,
∴BC=OC,
∴AB=AO=OB=OC=BC,
∴四边形AOCB为菱形;
(2)连接AC、AD,
∵AC=AD,AO=AO,OC=OD,
∴△AOC≌△AOD(SSS),
∴∠CAO=∠DAO=$\frac{1}{2}$∠CAO,
∵AB=AO=OB=OC=BC,
∴△ABO和△CBO是等边三角形,
∴∠OCB=∠OAB=60°,
∵四边形AOCB是菱形,
∴AC⊥OB,∠OAC=∠OCA=30°,
∴∠CAD=2∠OAC=60°,
∵OA=2,∠OAC=30°
∴AC=2$\sqrt{3}$,
∴S扇形CAD=$\frac{60π•(2\sqrt{3})^{2}}{360}$=2π,
∴S△AOC=$\frac{1}{2}$×$1×2\sqrt{3}$=$\sqrt{3}$,
∴S阴影=S扇形CAD-2S△AOC=2π-2$\sqrt{3}$.
点评 本题考查了圆周角定理、旋转的性质、扇形的面积公式、等边三角形的性质和判定、三角形全等的性质和判定、菱形的性质和判定,应用的知识较多,但难度不大,注意:所求的阴影部分是以A为圆心,以AC为半径的扇形CAD与两三角形面积的差.

 阅读快车系列答案
阅读快车系列答案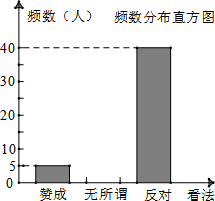 当前,“校园ipad现象已经受到社会的广泛关注,某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理:
当前,“校园ipad现象已经受到社会的广泛关注,某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理:频数分布表
| 看法 | 频数 | 频率 |
| 赞成 | 5 | 0.1 |
| 无所谓 | 5 | 0.1 |
| 反对 | 40 | 0.8 |
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
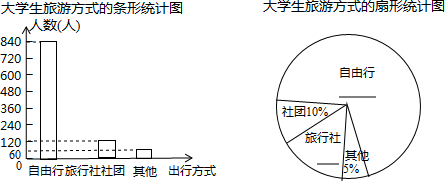
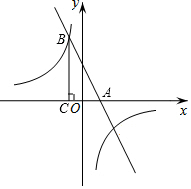 如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).
如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).