题目内容
14.对于正整数a,我们规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=$\frac{a}{2}$.例如f(15)=3×15+1=46,f(10)=$\frac{10}{2}$=5.若a1=8,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a3=2,a1+a2+a3+…+a2014=4705.分析 首先根据规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=$\frac{a}{2}$,算出a1=8,a2=4,a3=2,a4=1,a5=4,a6=2,a7=1,a8=4,…发现数据以“4,2,1”三个数循环出现,根据此规律计算即可.
解答 解:a1=8,a2=f(8)=$\frac{8}{2}$=4,a3=f(4)=$\frac{4}{2}$=2,a4=f(2)=$\frac{2}{2}$=1,a5=f(1)=3×1+1=4,a6=f(4)=2…
可知:a3=2,
从a2开始以“4,2,1”三个数循环出现,(2014-1)÷3=671,
故a1+a2+a3+…+a2014=8+(4+2+1)×671=4705.
故答案为:2,4705.
点评 此题主要考查新定义运算和数列规律的探索应用,根据新定义准确计算,结合计算结果发现存在的规律并加以应用是解题的关键.

练习册系列答案
相关题目
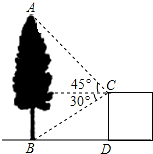 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)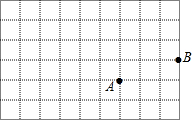 在正方形的网格中,每个小正方形的边长都为1,格点A、B的位置如图所示:
在正方形的网格中,每个小正方形的边长都为1,格点A、B的位置如图所示: