题目内容
已知函数y=-3（x-2）2+9．
（1）确定下列抛物线的开口方向、对称轴和顶点坐标；
（2）求出该抛物线与x轴的交点坐标及两交点间距离；
（3）求出该抛物线与y轴的交点坐标．
（1）确定下列抛物线的开口方向、对称轴和顶点坐标；
（2）求出该抛物线与x轴的交点坐标及两交点间距离；
（3）求出该抛物线与y轴的交点坐标．
考点：二次函数的性质,抛物线与x轴的交点
专题：
分析：（1）根据抛物线的解析式可以得到答案：
（2）令y=0，可以求得抛物线与x轴的交点坐标，然后利用两点间的距离公式可以求得两交点间距离；
（3）令x=0，即可求得相应的y的值．
（2）令y=0，可以求得抛物线与x轴的交点坐标，然后利用两点间的距离公式可以求得两交点间距离；
（3）令x=0，即可求得相应的y的值．
解答：解：（1）∵函数的解析式为：y=-3（x-2）2+9，且-3＜0，
∴抛物线的开口方向向下，对称轴是x=2，顶点坐标是（2，9）；
（2）令y=0，则-3（x-2）2+9=0，
整理，得（x-2）2=3，
开方，得x-2=±
，
解得，x1=2+
，x2=2-
，
所以，该抛物线与x轴的交点坐标是（2+
，0），（2-
，0），两点间的距离是|2+
-2+
|=2
；
（3）令x=0，则y=-3（0-2）2+9=-12+9=-3，即该抛物线与y轴的交点坐标是（0，-3）．
∴抛物线的开口方向向下，对称轴是x=2，顶点坐标是（2，9）；
（2）令y=0，则-3（x-2）2+9=0，
整理，得（x-2）2=3，
开方，得x-2=±
| 3 |
解得，x1=2+
| 3 |
| 3 |
所以，该抛物线与x轴的交点坐标是（2+
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
（3）令x=0，则y=-3（0-2）2+9=-12+9=-3，即该抛物线与y轴的交点坐标是（0，-3）．
点评：本题考查了二次函数的性质，抛物线与x轴的交点．求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．
练习册系列答案
相关题目
O的线路以每秒1个单位的速度向点O运动，当点P到达A点时，点Q也随之停止，设点P，Q运动的时间为t（秒）．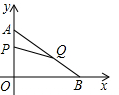
如图，在平面直角坐标系xOy内，已知点A（0，6）、点B（8，0），动点P从点O开始在线段OA上以每秒1个单位长度的速度向点A移动，同时动点Q从点A开始在线段AB上以每秒2个单位长度的速度向点B移动，设点P、Q移动的时间为t秒．