题目内容
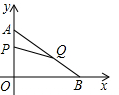 如图,在平面直角坐标系xOy内,已知点A(0,6)、点B(8,0),动点P从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,同时动点Q从点A开始在线段AB上以每秒2个单位长度的速度向点B移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系xOy内,已知点A(0,6)、点B(8,0),动点P从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,同时动点Q从点A开始在线段AB上以每秒2个单位长度的速度向点B移动,设点P、Q移动的时间为t秒.(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△ABO相似?
(3)当t为何值时,△APQ的面积为
| 32 |
| 5 |
考点:一次函数综合题
专题:代数几何综合题
分析:(1)设直线AB的解析式为y=kx+b(k≠0),解得k,b即可;
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t.②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
(3)(3)过点Q作QE垂直AO于点E.在Rt△AEQ中,QE=AQ•sin∠BAO=
(6-t)•
即可得出结论.
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t.②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
(3)(3)过点Q作QE垂直AO于点E.在Rt△AEQ中,QE=AQ•sin∠BAO=
| 1 |
| 2 |
| 8t |
| 5 |
解答:解:(1)解:(1)设直线AB的解析式为y=kx+b,
由题意,得
,
解得
,
所以,直线AB的解析式为y=-
x+6;
(2)∵AO=6,BO=8,
∴AB=10,
∴AP=6-t,AQ=2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以
=
,即
=
,解得t=3(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
∴
=
,即
=
,解得t=
(秒);
∴当t为3秒或
秒时,△APQ与△AOB相似;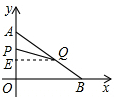
(3)过点Q作QE垂直AO于点E.
在Rt△AOB中,sin∠BAO=
=
,
在Rt△AEQ中,QE=AQ•sin∠BAO=2t•
=
,
S△APQ=
AP•QE=
(6-t)•
,
=-
t2+
=
,
解得t=3+
(秒)或t=3-
(秒).
∴当t=3+
秒或3-
秒时,△APQ的面积为
个平方单位
由题意,得
|
解得
|
所以,直线AB的解析式为y=-
| 3 |
| 4 |
(2)∵AO=6,BO=8,
∴AB=10,
∴AP=6-t,AQ=2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以
| AP |
| OA |
| AQ |
| AB |
| 6-t |
| 6 |
| 2t |
| 10 |
②当∠AQP=∠AOB时,△AQP∽△AOB.
∴
| AQ |
| OA |
| AP |
| AB |
| 2t |
| 6 |
| 6-t |
| 10 |
| 9 |
| 5 |
∴当t为3秒或
| 9 |
| 5 |

(3)过点Q作QE垂直AO于点E.
在Rt△AOB中,sin∠BAO=
| OB |
| AB |
| 4 |
| 5 |
在Rt△AEQ中,QE=AQ•sin∠BAO=2t•
| 4 |
| 5 |
| 8t |
| 5 |
S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 8t |
| 5 |
=-
| 4 |
| 5 |
| 24t |
| 5 |
| 32 |
| 5 |
解得t=3+
| 15 |
| 15 |
∴当t=3+
| 15 |
| 15 |
| 32 |
| 5 |
点评:本题考查的是一次函数综合题,根据题意作出辅助线.构造出相似三角形是解答此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
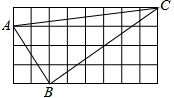 如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识回答问题.
如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识回答问题. 已知:如图,?ABCD中,AD=2AB,将CD向两边分别延长到E,F使CD=CE=DF.求证:AE⊥BF.
已知:如图,?ABCD中,AD=2AB,将CD向两边分别延长到E,F使CD=CE=DF.求证:AE⊥BF.