题目内容
12.如图1,△ABC是等腰直角三角形,∠ACB=90°,点P是AB上一点,以CP为斜边作等腰直角△CPE,连接AE并延长交BC的延长线于点D(1)试判断∠BPC与∠ECD的关系,并说明理由;
(2)如图2,过C点作CM⊥AB于M点,连接ME,试证明ME垂直平分AC;
(3)在点P在AB上运动的过程中(P不与A、B重合),AP、BP、CP之间存在着某种数量关系,请直接写出它们之间的数量关系(结论不需要证明)
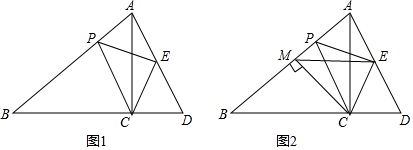
分析 (1)由∠PCD=∠B+∠BPC=∠PCE+∠ECD可知,只要证明∠B=∠PCE=45°即可.
(2)如图2中,作EK⊥AB于K,EH⊥CM于H.由△EKP≌△EHC,推出EK=EH,因为EK⊥AB于K,EH⊥CM于H.所以∠EMK=∠EMC=45°,推出∠AME=∠B,推出ME∥BC,由CA=CB,CM⊥AB,推出AM=BM,CM=AM=BM,推出AE=ED,在Rt△ACD中,EC=AE=ED,此MA=MC,由此推出ME垂直平分线段AC.
(3)结论:PB2+AP2=2PC2.如图3中,将△ACP绕点C逆时针旋转90°得到△BCN.由∠ABC=∠CBN=45°,推出∠PBN=90°,推出PB2+BN2=PN2,由PC=CN,∠ACP=∠BCN,推出∠PCN=∠ACB=90°,推出PN=$\sqrt{2}$PC,AN=BN,即可推出PB2+AP2=2PC2.
解答 (1)解:结论:∠BPC=∠ECD.
理由:如图1中,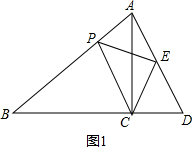
∵CA=CB,∠ACB=90°,
∴∠B=∠CAB=45°,
∵EP=EC,∠PEC=90°,
∴∠EPC=∠ECP=45°,
∵∠PCD=∠B+∠BPC=∠PCE+∠ECD,
∵∠B=∠PCE=45°,
∴∠BPC=∠ECD.
(2)证明:如图2中,作EK⊥AB于K,EH⊥CM于H.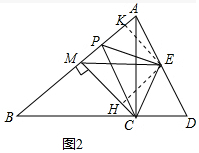
∵∠PMC+∠PEC=180°,
∴∠MPE+∠ECH=180°,
∵∠EPK+∠MPE=180°,
∴∠EPK=∠ECH,
∵∠EKP=∠EHC=90°,EP=EC,
∴△EKP≌△EHC,
∴EK=EH,∵EK⊥AB于K,EH⊥CM于H.
∴∠EMK=∠EMC=45°,
∴∠AME=∠B,
∴ME∥BC,
∵CA=CB,CM⊥AB,
∴AM=BM,CM=AM=BM,
∴AE=ED,
在Rt△ACD中,EC=AE=ED,
∵MA=MC,
∴ME垂直平分线段AC.
(3)解:结论:PB2+AP2=2PC2.
理由:如图3中,将△ACP绕点C逆时针旋转90°得到△BCN.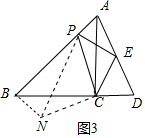
则∵∠ABC=∠CBN=45°,
∴∠PBN=90°,
∴PB2+BN2=PN2,
∵PC=CN,∠ACP=∠BCN,
∴∠PCN=∠ACB=90°,
∴PN=$\sqrt{2}$PC,AN=BN,
∴PB2+AP2=2PC2.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、角平分线的判定定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用旋转法添加辅助线构造全等三角形,属于中考压轴题.

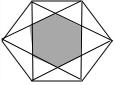 如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
| A. | 若|a|=-a,则a<0 | B. | 若a<0,ab<0,则b>0 | ||
| C. | 若ab>0,则a>0,b>0 | D. | 若a=b,m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$ |
 一次函数y=kx+b的图象如图所示,当x>0时,y的取值范围为y>-4.
一次函数y=kx+b的图象如图所示,当x>0时,y的取值范围为y>-4.