题目内容
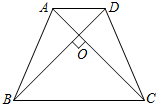 如图,在等腰梯形ABCD中,已知AD∥BC,对角线AC与BD互相垂直,且AD=30,BC=70,求BD的长.
如图,在等腰梯形ABCD中,已知AD∥BC,对角线AC与BD互相垂直,且AD=30,BC=70,求BD的长.考点:等腰梯形的性质,勾股定理,平行四边形的判定与性质
专题:
分析:首先过点D作DE∥AC交BC延长线于点E,可得四边形ACED是平行四边形.则可求得BE的长,然后由在等腰梯形ABCD中,得到DB=AC=DE,又由对角线AC与BD互相垂直,利用勾股定理求得答案.
解答: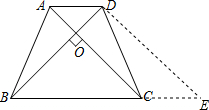 解:过点D作DE∥AC交BC延长线于点E,
解:过点D作DE∥AC交BC延长线于点E,
∵AD∥BE,DE∥AC,
∴四边形ACED是平行四边形.
∴CE=AD=30,DE=AC,
∴BE=BC+CE=BC+AD=100.
∵在等腰梯形ABCD中,
∴DB=AC=DE,
∵AC与BD互相垂直,
∴∠BOC=90°.
∵DE∥AC,
∴∠BDE=∠BOC=90°,
∴在Rt△BDE中,∠BDE=90°,
∴BD2+DE2=BE2,
∴2BD2=BE2,
∴BD=50
.
 解:过点D作DE∥AC交BC延长线于点E,
解:过点D作DE∥AC交BC延长线于点E,∵AD∥BE,DE∥AC,
∴四边形ACED是平行四边形.
∴CE=AD=30,DE=AC,
∴BE=BC+CE=BC+AD=100.
∵在等腰梯形ABCD中,
∴DB=AC=DE,
∵AC与BD互相垂直,
∴∠BOC=90°.
∵DE∥AC,
∴∠BDE=∠BOC=90°,
∴在Rt△BDE中,∠BDE=90°,
∴BD2+DE2=BE2,
∴2BD2=BE2,
∴BD=50
| 2 |
点评:此题考查了等腰梯形的性质、平行四边形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
一筐苹果4千克,增加
后,列出的算式为( )
| 1 |
| 2 |
A、4+
| ||
B、4×(1+
| ||
| C、4÷(1+) | ||
D、4×(1-
|
一组数据中的每个数都加10,则①平均数加10;②中位数不变;③极差加10;④方差不变.其中正确的说法有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.
如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.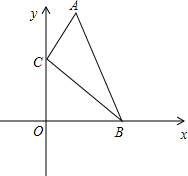 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.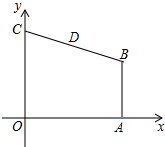 已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点.动点P从点A出发,以每秒4个单位的速度,沿折线AO-OC-CD向终点D运动,设运动时间为t秒.
已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点.动点P从点A出发,以每秒4个单位的速度,沿折线AO-OC-CD向终点D运动,设运动时间为t秒. 已知:如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于点E,交AC于点F,若BE+CF=9cm,求线段EF的长.
已知:如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于点E,交AC于点F,若BE+CF=9cm,求线段EF的长.