题目内容
 如图,在△ABC中,∠ABC=∠ACB,P是△ABC内一点,∠BPC=100°,且∠1=∠2.则∠A=
如图,在△ABC中,∠ABC=∠ACB,P是△ABC内一点,∠BPC=100°,且∠1=∠2.则∠A=考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理求出∠2+∠PCB的度数,再根据∠ABC=∠ACB,∠1=∠2,可知∠2+∠PCB=∠1+∠PCB=∠2+∠PBC,再由三角形内角和定理即可得出结论.
解答:解:∵△BCP中,∠BPC=100°,
∴∠2+∠PCB=180°-100°=80°.
∵∠ABC=∠ACB,∠1=∠2,
∴∠2+∠PCB=∠1+∠PCB=∠2+∠PBC=80°,即∠ABC=∠ACB=80°,
∴∠A=180°-∠ABC-∠ACB=180°-80°-80°=20°.
故答案为:20°.
∴∠2+∠PCB=180°-100°=80°.
∵∠ABC=∠ACB,∠1=∠2,
∴∠2+∠PCB=∠1+∠PCB=∠2+∠PBC=80°,即∠ABC=∠ACB=80°,
∴∠A=180°-∠ABC-∠ACB=180°-80°-80°=20°.
故答案为:20°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
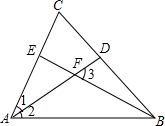 如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )| A、59° | B、60° |
| C、56° | D、22° |
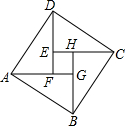 如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )
如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )| A、1:5 | B、1:25 |
| C、5:1 | D、25:1 |
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
关于x的一元二次方程kx2-x+1=0有两个不相等的实数根,则k的取值范围是( )
A、k<
| ||
B、k>
| ||
C、k<
| ||
D、k>
|
 如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.
如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.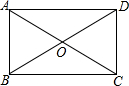 如图,在矩形ABCD中,对角线AC、BD相交于O,AB=OA=3,则BC=
如图,在矩形ABCD中,对角线AC、BD相交于O,AB=OA=3,则BC=