题目内容
19.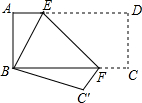 如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠AEB的度数是70°.
如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠AEB的度数是70°.
分析 由折叠的性质可求得∠EFC=∠EFC′=125°,由平行线的性质可求得∠DEF=∠BEF=55°,从而可求得∠AEB的度数.
解答 解:
由折叠的性质可得∠EFC=∠EFC′=125°,∠DEF=∠BEF,
∵AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠DEF=∠BEF=180°-∠EFC=180°-125°=55°,
∴∠AEB=180°-∠DEF-∠BEF=180°-55°-55°=70°,
故答案为:70°.
点评 本题主要考查平行线和折叠的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
9. 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )| A. | AB=CD | B. | AO=CO | C. | AC=BD | D. | BO=DO |
14.下列说法中正确的是( )
| A. | 旋转一定会改变图形的形状和大小 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 相等的角是对顶角 |
8. 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
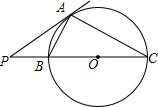 如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.
如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.