题目内容
10.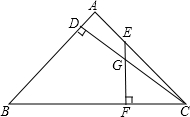 △ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
△ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
分析 过点A作AP⊥BC于P,交CD于H,由EF⊥BC,得到AP∥EF,于是推出△CEG∽△CAH,△CGF∽△CPH,得到$\frac{EG}{AH}=\frac{AH}{CP}=\frac{1}{2}$,又由于△BDC∽△ADH,得到$\frac{AD}{CD}=\frac{AH}{BC}$,根据AB=AC推出BC=2PC,得到$\frac{AD}{CD}=\frac{1}{4}$,于是得到结果.
解答 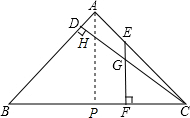 解:过点A作AP⊥BC于P,交CD于H,
解:过点A作AP⊥BC于P,交CD于H,
∵EF⊥BC,
∴AP∥EF,
∴△CEG∽△CAH,△CGF∽△CPH,
∴$\frac{EG}{AH}=\frac{CG}{CH}$,$\frac{CG}{CH}=\frac{CF}{CP}$,
∴$\frac{EG}{AH}=\frac{CF}{CP}$,
∴$\frac{EG}{CF}=\frac{AH}{CP}$,
∵EG=$\frac{1}{2}$CF,
∴$\frac{EG}{CF}=\frac{AH}{CP}$=$\frac{1}{2}$,
∵∠B+∠BAH=∠DAH+∠BAH=90°,
∴∠B=∠DHA,
∴△BDC∽△ADH,
∴$\frac{AD}{CD}=\frac{AH}{BC}$,
∵AB=AC,
∴BC=2PC,
∴$\frac{AD}{CD}=\frac{1}{4}$,
设AD=k,CD=4k,则AC=AB=$\sqrt{17}k$,
∴BD=$\sqrt{17}k-k$,
∴$\frac{AD}{BD}=\frac{1}{\sqrt{17}-1}=\frac{\sqrt{17}+1}{16}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20.若a2=25,|b|=3,则a+b=( )
| A. | 8 | B. | ±8 | C. | ±2 | D. | ±8或±2 |
2.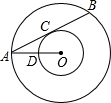 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
19.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
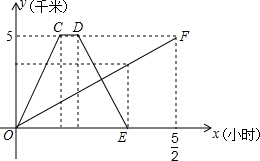 A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
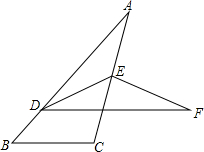 如图,在△ABC中,点D、E分别是AB、AC上的点,将△ABC沿DE折叠,点A落到F的位置,已知DF∥BC,∠B=50°,∠CEF=80°,说明:EA=ED.
如图,在△ABC中,点D、E分别是AB、AC上的点,将△ABC沿DE折叠,点A落到F的位置,已知DF∥BC,∠B=50°,∠CEF=80°,说明:EA=ED.
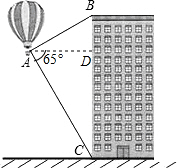 如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)