题目内容
2.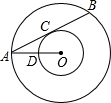 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
分析 连接OC,利用切线的性质知OC⊥AB,由垂径定理得AB=2AC,因为tan∠OAB=$\frac{1}{2}$,易得$\frac{OC}{AC}$=$\frac{1}{2}$,代入得结果.
解答  解:连接OC,
解:连接OC,
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∴AB=2AC,
∵OD=2,
∴OC=2,
∵tan∠OAB=$\frac{1}{2}$,
∴AC=4,
∴AB=8,
故选C.
点评 本题主要考查了切线的性质和垂径定理,连接过切点的半径是解答此题的关键.

练习册系列答案
相关题目
12. 如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
 如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )| A. | 100° | B. | 108° | C. | 110° | D. | 120° |
12.已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
| A. | t=20v | B. | t=$\frac{20}{v}$ | C. | t=$\frac{v}{20}$ | D. | t=$\frac{10}{v}$ |
 如图,已知长方形纸片ABCD,AB=CD,AD=BC,现将长方形纸片ABCD沿对角线AC对折,使点B落在点E处,试说明DF=EF.
如图,已知长方形纸片ABCD,AB=CD,AD=BC,现将长方形纸片ABCD沿对角线AC对折,使点B落在点E处,试说明DF=EF.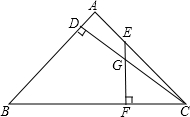 △ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
△ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.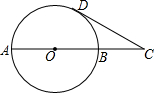 如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.
如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.
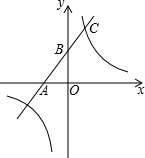 如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.