题目内容
1.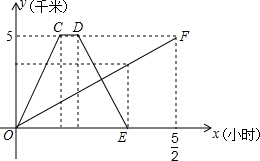 A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题:(1)求甲、乙两人的速度;
(2)求甲从B地返回到A地的过程中,y与x之间的函数关系式;
(3)甲、乙两人经过几个小时相遇?
分析 (1)由函数图象可知乙$\frac{5}{2}$小时行驶5千米,根据路程÷时间求出乙行驶的速度,再由当甲返回到A地时,乙距B地1.5千米,求出此时乙行驶的时间,减去在B地停留十分钟的时间就是甲行驶5×2=10千米的时间,进而得到甲的速度;
(2)设甲从B地返回到A地的过程中,y与x之间的函数关系式为y=kx+b,将D($\frac{23}{24}$,5),E($\frac{7}{4}$,0)代入,运用待定系数法即可求解;
(3)由图象可知,甲在DE段与乙相遇,联立两函数解析式得到方程组,解方程组即可.
解答 解:(1)由题意,得5÷$\frac{5}{2}$=2(km/h).
∴乙的速度为2km/h,
∴直线OF的解析式为y=2x,
∵当甲返回到A地时,乙距B地1.5千米,
∴5-1.5=3.5,
∴3.5=2x,解得x=$\frac{7}{4}$,
∴5×2÷($\frac{7}{4}$-$\frac{1}{6}$)=$\frac{120}{19}$,
∴甲的速度为$\frac{120}{19}$km/h;
(2)设甲从B地返回到A地的过程中,y与x之间的函数关系式为y=kx+b.
D点横坐标为($\frac{7}{4}$-$\frac{1}{6}$)÷2+$\frac{1}{6}$=$\frac{23}{24}$,
将D($\frac{23}{24}$,5),E($\frac{7}{4}$,0)代入,
得$\left\{\begin{array}{l}{\frac{23}{24}k+b=5}\\{\frac{7}{4}k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{120}{19}}\\{b=\frac{210}{19}}\end{array}\right.$,
∴甲从B地返回到A地的过程中,y与x之间的函数关系式为y=-$\frac{120}{19}$x+$\frac{210}{19}$;
(3)由$\left\{\begin{array}{l}{y=-\frac{120}{19}x+\frac{210}{19}}\\{y=2x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{105}{79}}\\{y=\frac{210}{79}}\end{array}\right.$,
故甲、乙两人经过$\frac{105}{79}$小时相遇.
点评 本题考查了一次函数的应用,行程问题的数量关系路程÷时间=速度的运用,待定系数法求一次函数的解析式的运用,两函数交点坐标求法的应用,难度适中.求出求出甲的速度是解题的关键.

 实数a,b在数轴上的位置如图所示,则化简$\sqrt{(a-1)^{2}}$-$\sqrt{(a-b)^{2}}$+b的结果是( )
实数a,b在数轴上的位置如图所示,则化简$\sqrt{(a-1)^{2}}$-$\sqrt{(a-b)^{2}}$+b的结果是( )| A. | 1 | B. | b+1 | C. | 2a | D. | 1-2a |
 如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )| A. | 100° | B. | 108° | C. | 110° | D. | 120° |
| 农作物 | 每公顷所需工人数/人 | 每公顷预计产值/万元 |
| 水稻 | 4 | 4.5 |
| 蔬菜 | 8 | 9 |
| 棉花 | 5 | 7.5 |
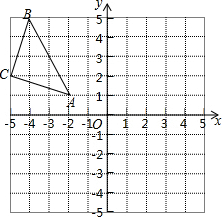 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2). 如图,已知长方形纸片ABCD,AB=CD,AD=BC,现将长方形纸片ABCD沿对角线AC对折,使点B落在点E处,试说明DF=EF.
如图,已知长方形纸片ABCD,AB=CD,AD=BC,现将长方形纸片ABCD沿对角线AC对折,使点B落在点E处,试说明DF=EF.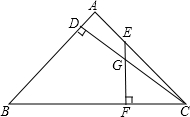 △ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
△ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.