题目内容
20.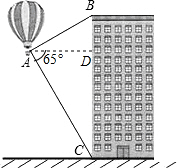 如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
分析 要求楼高BC,即求出BD、CD的长度,分别在Rt△ABD和Rt△ADC中求出BD和CD的长度,继而可求解.
解答 解:在Rt△ABD中,
∵tan∠BAD=$\frac{BD}{AD}$,
∴BD=ADtan30°=120×$\frac{\sqrt{3}}{3}$=40$\sqrt{3}$(米),
在Rt△ADC中,
∵tan∠CAD=$\frac{CD}{AD}$,
∴CD=ADtan65°=120tan65°,
∴BC=BD+CD=40$\sqrt{3}$+120tan65°.
答:这栋高楼的高度为(40$\sqrt{3}$+120tan65°)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
12.已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
| A. | t=20v | B. | t=$\frac{20}{v}$ | C. | t=$\frac{v}{20}$ | D. | t=$\frac{10}{v}$ |
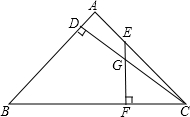 △ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
△ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
 如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是65°.
如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是65°.