题目内容
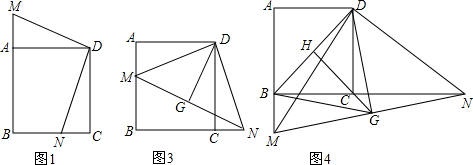
15.已知四边形ABCD是正方形(1)如图1.点M在边BA的延长线上,点N在边BC上,且AM=CN,连接MN,DM,DN,判断△DMN的形状(直接写出答案).
(2)如图2,当店N在边AB上,点N在边BC的延长线上,AM=CN,连接MN,取线段MN的中点G,连接DG,DM,判断线段DG和线段MG的关系并说明理由.
(3)如图3,当点M在边AB的延长线上,点N在边BC的延长线上,AM=CN,连接MN,DM,DN,点G是线段MN的中点,连接BG,DG,连接GC并延长交BD于点H,若∠AMN=75°,判断线段GH和线段BD的关系并说明理由.
分析 (1)由正方形的性质就可以得出AD=CD,∠MAD=∠C=∠ADC=90°,就可以得出△MAD≌△NCD,就可以得出MD=ND,∠ADM=∠CDN,就可以得出∠MDN=90°,进而得出结论;
(2)由正方形的性质就可以得出AD=CD,∠MAD=∠BCD=∠ADC=∠DCN=90°,就可以得出△MAD≌△NCD,就可以得出MD=ND,∠ADM=∠CDN,就可以得出∠MDN=90°,就可以得出△MDN为等腰直角三角形,由等腰直角三角形的性质就可以得出结论;
(3)由正方形的性质就可以得出AD=BC=CD,∠MAD=∠BCD=∠NCD=∠MBN=90°,就可以得出△MAD≌△NCD,就可以得出MD=ND,∠ADM=∠CDN,就可以得出∠MDN=90°,由直角三角形的性质就可以得出BG=DG,等腰直角三角形的性质就可以得出∠MGD=90°.由∠AMN=75°就可以得出∠MCB=30°,得出∠BGD=60°,得出△BGD为等边三角形,进而由△BCG≌△DCG就可以得出∠BGC=∠DGC=30°,就有GH⊥BD,由勾股定理就可以求出结论.
解答 解:(1)△DMN的形状是等腰直角三角形.
理由:∵四边形ABCD是正方形,
∴AD=CD,∠MAD=∠C=∠ADC=90°.
在△MAD和△NCD中
$\left\{\begin{array}{l}{AD=CD}\\{∠MAD=∠C}\\{AM=CN}\end{array}\right.$,
∴△MAD≌△NCD(SAS),
∴MD=ND,∠ADM=∠CDN.
∵∠ADN+∠CDN=∠ADC=90°,
∴∠ADN+∠ADM=90°,
即∠MDN=90°,
∴△DMN是等腰直角三角形;
(2)DG=MG,DG⊥MG.
理由:∵四边形ABCD是正方形,
∴AD=CD,∠MAD=∠BCD=∠NCD=90°.
在△MAD和△NCD中
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCN}\\{AM=CN}\end{array}\right.$,
∴△MAD≌△NCD(SAS),
∴MD=ND,∠ADM=∠CDN.
∵∠ADN+∠CDM=∠ADC=90°,
∴∠CDN+∠CDM=90°,
即∠MDN=90°,
∴△DMN是等腰直角三角形.
∵G是MN的中点,
∴MG=$\frac{1}{2}$MN,DG=$\frac{1}{2}$MN,DG⊥MG,
∴DG=MG,DG⊥M;
(3)GH⊥BD,GH:BD=$\sqrt{3}$:2.
理由:∵四边形ABCD是正方形,
∴AD=BC=CD,∠MAD=∠BCD=∠NCD=∠MBN=90°.
在△MAD和△NCD中
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCN}\\{AM=CN}\end{array}\right.$,
∴△MAD≌△NCD(SAS),
∴MD=ND,∠ADM=∠CDN.
∵∠ADM+∠CDM=∠ADC=90°,
∴∠CDN+∠CDM=90°,
即∠MDN=90°
∴△DMN是等腰直角三角形.
∵G是线段MN的中点,
∴DG⊥MN,DG=$\frac{1}{2}$MN,BG=$\frac{1}{2}$MN,MG=$\frac{1}{2}$MN
∴∠MGD=90°,DG=BG=MG.
∴∠GBM=∠BMG.
∵∠AMN=75°,
∴∠GBM=75°,
∴∠MGB=30°,
∴∠BGD=60°.
∴△BGD为的年三角形.
在△BCG和△DCG中
$\left\{\begin{array}{l}{BC=DC}\\{BG=DG}\\{CG=CG}\end{array}\right.$,
∴△BCG≌△DCG(SSS),
∴∠BGC=∠DGC=30°,
∴GH⊥BD,BH=DH=$\frac{1}{2}$BD.
设BH=DH=x,则BD=BG=2x,由勾股定理,得
GH=$\sqrt{3}$x.
∴GH:BD=$\sqrt{3}$:2.
点评 本题考查了正方形的性质的运用,等腰直角三角形的判定及性质的运用,等边三角形的判定及性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是解答本题的关键.

| 农作物 | 每公顷所需工人数/人 | 每公顷预计产值/万元 |
| 水稻 | 4 | 4.5 |
| 蔬菜 | 8 | 9 |
| 棉花 | 5 | 7.5 |
| A. | 正五边形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
 如图,∠A=60°,DF⊥AB于F,DG∥AC交AB于G,DE∥AB交AC于E.求∠GDF的度数.
如图,∠A=60°,DF⊥AB于F,DG∥AC交AB于G,DE∥AB交AC于E.求∠GDF的度数.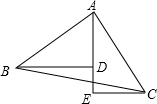 如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.
如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.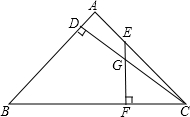 △ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.
△ABC中,AB=AC,CD⊥AB于D,E是AC上动点,EF⊥BC于F,交CD于G,若EG=$\frac{1}{2}$CF,则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$.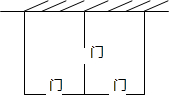 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.