题目内容
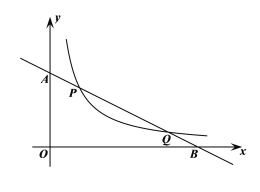
【题目】二次函数
的函数图象如图，点
位于坐标原点，点
在
轴的正半轴上，点
在二次函数位于第一象限的图象上，
，
，
，
…都是直角顶点在抛物线上的等腰直角三角形，则
的斜边长为( )
A.20B.
C.22D.
【答案】C
【解析】
由于
,
,
，…，都是等腰直角三角形，因此可得出直线
:
，求出
，
的坐标，得出
的长；
利用 的坐标，得直线
：
，求出
,
坐标，得出
的长；用同样的的方法可求得
，…的边长，然后根据各边长的的特点得出一般化规律，求得
的长．
解：
等腰直角三角形，
为原点；
直线：
，
， 的坐标为（1，1），则 为（0，2）
=2
为（0，2），直线 :
（2，4），=4，则（0，6）
（0，6），直线
:
（3，9）， =6，
由上面A0A1=2，A1A2=4，A2A3=6，可以看出这些直角顶点在抛物线上的等腰直角三角形的斜边长依次加2
∴△A10B11A11的斜边长为2+10×2=22，
综上，由此可以推出=22．
故选C．
练习册系列答案
教材全解字词句篇系列答案
相关题目
