题目内容
【题目】在正方形![]() 中,
中,![]() 是一条对角线,点
是一条对角线,点![]() 在直线
在直线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,平移
,平移![]() ,使点
,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
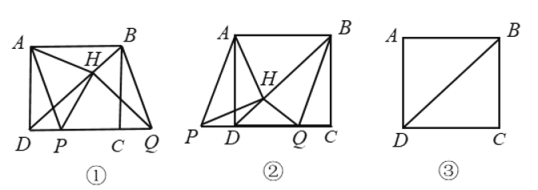
(问题发现)
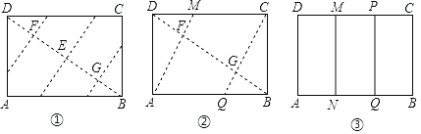
(1)如图①,若点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 的数量关系是________,位置关系是________.
的数量关系是________,位置关系是________.
(拓展探究)
(2)如图②,若点![]() 在线段
在线段![]() 的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
(解决问题)
(3)若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,正方形
,正方形![]() 的边长为2,请直接写出求
的边长为2,请直接写出求![]() 的长度.
的长度.
【答案】(1)![]() ,
,![]() ;(2)结论仍然成立,理由见解析;(3)
;(2)结论仍然成立,理由见解析;(3)![]() .
.
【解析】
(1)连接HC,根据正方形的性质、等腰直角三角形的性质得到△HDP≌△HQC,根据全等三角形的性质得到HP=HC,∠DHP=∠QHC,根据正方形是轴对称图形证明结论;
(2)同(1)的证明方法相同,根据图形证明即可;
(3)由(1)的结论AH=PH,AH⊥PH,得出∠HPA=45°,推导出∠APD=30°,再由三角函数即可求解.
(1)![]() ,
,![]() .
.
证明如下:如解图,连接![]() ,
,
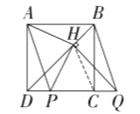
∵四边形![]() 是正方形,
是正方形,
∴∠![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
由平移的性质可知![]() ,
,
在![]() 和
和![]() 中,
中,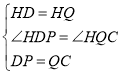 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
根据正方形是轴对称图形得到![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,![]() .
.
故答案为:![]() ,
,![]() ;
;
(2)(1)中的结论仍然成立,
理由如下:如解图,连接![]() ,
,

∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
由平移的性质可知![]() ,
,
在![]() 和
和![]() 中,
中,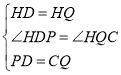 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
根据正方形是轴对称图形得到![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(3)![]() .
.
由(1)知,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.

 亮点激活精编提优100分大试卷系列答案
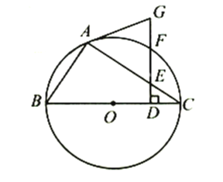
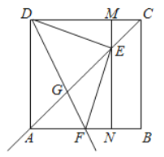
亮点激活精编提优100分大试卷系列答案【题目】如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?
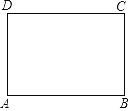
以下是小红的研究过程.
思考过程 | 要使边AB被三等分,若从边DC上考虑,就是要折出DM= 也就是要折出DM= 当DB、AM相交于F时,即要折出对角线上的DF= |
折叠方法和示意图 | ①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G; ②折出AF、CG,分别交边CD、AB于M、Q; ③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分.
|
(1)整理小红的研究过程,说明AN=NQ=QB;
(2)用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)