题目内容
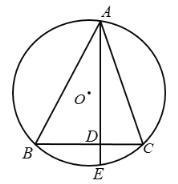
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长是_________.
的长是_________.
【答案】![]()
【解析】
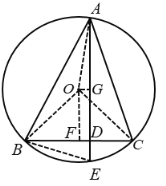
连结OB,OC,OA,过O点作OF⊥BC于F,作OG⊥AE于G,根据圆周角定理可得∠BOC=90°,根据等腰直角三角形的性质和勾股定理可得DG,AG,可求AD,再根据相似三角形的判定和性质可求DE.
解:连结OB,OC,OA,过O点作OF⊥BC于F,作OG⊥AE于G,
∵⊙O是△ABC的外接圆,∠BAC=45°,
∴∠BOC=90°,
∵BD=4,CD=1,
∴BC=4+1=5,
∴OB=OC=![]() ,
,
∴OA=![]() ,OF=BF=
,OF=BF=![]() ,
,
∴DF=BDBF=![]() ,
,
∴OG=![]() ,GD=
,GD=![]() ,
,
在Rt△AGO中,AG=![]() ,
,
∴AD=AG+GD=![]() ,
,
∵连接BE,AD与BE相交于D,
∴∠BED=∠ACD,∠BDE=∠ADC,
∴△BDE∽△ADC,
∴![]()
 .
.
故答案为:![]() .
.

练习册系列答案
相关题目