ћвƒњƒЏ»Ё
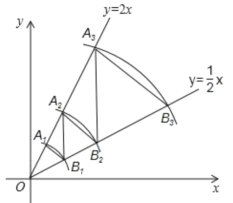
°Њћвƒњ°њ∆п–– «ѕ÷‘ЏЅч––µƒљ°…нЈљ љ÷Ѓ“ї£ђ÷№ƒ©°∞¬ћ…Ђ∆п––Њгј÷≤њ°±„й÷ѓЅЋ“їіќі”Љ„µЎ≥цЈҐ£ђƒњµƒµЎќ™““µЎµƒ∆п––їоґѓ£ђ‘Џ°∞Њгј÷≤њ°±„‘––≥µґ”≥цЈҐ1–° ±Їу£ђ«°”–“їЅЊƒ¶Ќ–≥µі”Љ„µЎ≥цЈҐ£ђ—Ў„‘––≥µґ”––љш¬Јѕя«∞Ќщ““µЎ£ђµљіп““µЎЇуЅҐЉі∞і‘≠¬ЈЈµїЎЉ„µЎ£Ѓ„‘––≥µґ””лƒ¶Ќ–≥µ–– їЋўґ»Њщ±£≥÷≤ї±д£ђ≤Ґ«“ƒ¶Ќ–≥µ–– їЋўґ» «„‘––≥µґ”–– їЋўґ»µƒ3±ґ£Ѓ»зЌЉЋщ Њµƒ «„‘––≥µґ”°Ґƒ¶Ќ–≥µјлЉ„µЎµƒ¬Ј≥ћ![]() ”л„‘––≥µґ”јлњ™Љ„µЎµƒ ±Љд
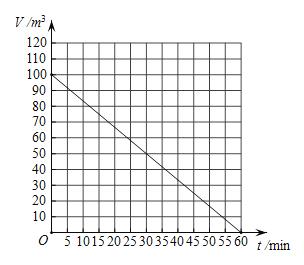
”л„‘––≥µґ”јлњ™Љ„µЎµƒ ±Љд![]() µƒєЎѕµЌЉѕу£ђ«лЄщЊЁЌЉѕућбє©µƒ–≈ѕҐ£ђїЎірѕ¬Ѕ–ќ ћв£Ѓ
µƒєЎѕµЌЉѕу£ђ«лЄщЊЁЌЉѕућбє©µƒ–≈ѕҐ£ђїЎірѕ¬Ѕ–ќ ћв£Ѓ
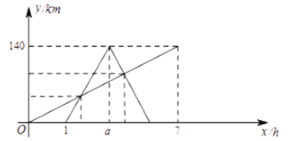
£®1£©ƒ¶Ќ–≥µ–– їµƒЋўґ» «__________£ї![]() ____________£ї
____________£ї
£®2£©«у≥ц„‘––≥µґ”јлЉ„µЎµƒ¬Ј≥ћ![]() ”л„‘––≥µґ”јлњ™Љ„µЎµƒ ±Љд
”л„‘––≥µґ”јлњ™Љ„µЎµƒ ±Љд![]() µƒєЎѕµ љ£ђ≤Ґ«у≥ц„‘––≥µґ”≥цЈҐґа…ў–° ±”лƒ¶Ќ–≥µѕа”ц£ї
µƒєЎѕµ љ£ђ≤Ґ«у≥ц„‘––≥µґ”≥цЈҐґа…ў–° ±”лƒ¶Ќ–≥µѕа”ц£ї
£®3£©÷±љ”–і≥цµ±ƒ¶Ќ–≥µ”л„‘––≥µґ”ѕаЊа![]() ±£ђіЋ ±јлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋґа…ў–° ±£Ѓ
±£ђіЋ ±јлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋґа…ў–° ±£Ѓ
°Њір∞Є°њ£®1£©![]() £ї
£ї![]() £ї£®2£©
£ї£®2£©![]() £ђ„‘––≥µґ”≥цЈҐЇу
£ђ„‘––≥µґ”≥цЈҐЇу![]() –° ±їт
–° ±їт![]() –° ±”л„‘––≥µґ”ѕа”ц£ї£®3£©ƒ¶Ќ–≥µ”л„‘––≥µґ”ѕаЊа
–° ±”л„‘––≥µґ”ѕа”ц£ї£®3£©ƒ¶Ќ–≥µ”л„‘––≥µґ”ѕаЊа![]() ±£ђіЋ ±јлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋ
±£ђіЋ ±јлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋ![]() –° ±їт
–° ±їт![]() –° ±їт
–° ±їт![]() –° ±їт
–° ±їт![]() –° ±£Ѓ
–° ±£Ѓ
°Њљвќц°њ
£®1£©”…Ћўґ»![]() ¬Ј≥ћ
¬Ј≥ћ![]() ±Љд£ђ ±Љд
±Љд£ђ ±Љд![]() ¬Ј≥ћ
¬Ј≥ћ![]() Ћўґ»њ…“‘«у≥цљб¬џ£ї
Ћўґ»њ…“‘«у≥цљб¬џ£ї
£®2£©”…„‘––≥µµƒЋўґ»ЊЌњ…“‘«у≥цƒ¶Ќ–≥µµƒЋўґ»£ђ‘ў”…„ЈЉ∞ќ ћв…и„‘––≥µ≥µ≥цЈҐ![]() –° ±Ѕљ≥µѕа”цљ®ЅҐЈљ≥ћ«у≥ц∆дљвЉіњ…£ї
–° ±Ѕљ≥µѕа”цљ®ЅҐЈљ≥ћ«у≥ц∆дљвЉіњ…£ї
£®3£©Ј÷«йњцћ÷¬џ£ђ«у≥цƒ¶Ќ–≥µ‘ЏЈµ≥ћЌЊ÷–”л„‘––≥µґ”‘ўіќѕа”ц ±µƒ ±Љд£ђЉіњ…µ√≥цЊајлЉ„µЎµƒ¬Ј≥ћ£Ѓ
љв£Ї£®1£©„‘––≥µґ”–– їµƒЋўґ»ќ™![]()
‘тƒ¶Ќ–≥µ–– їµƒЋўґ»ќ™![]()
![]()
є ір∞Є![]() £ї
£ї![]()
£®2£©…и„‘––≥µґ”≥цЈҐx–° ±”лƒ¶Ќ–≥µѕа”ц£ђ„‘––≥µґ”µƒЇѓ эєЎѕµ љќ™£Ї![]() £ђ
£ђ
ЄщЊЁЌЉѕсњ…µ√£Ї![]() £ђ
£ђ
°а![]()
°а„‘––≥µґ”µƒЇѓ эєЎѕµ љќ™£Ї![]() £ђ£ђ
£ђ£ђ
Ґў „іќѕа”ц ”…ћв“вµ√![]() £ђљвµ√
£ђљвµ√![]()
ҐЏƒ¶Ќ–≥µ‘ЏЈµ≥ћ÷–”л„‘––≥µґ”‘ўіќѕа”ц
ЄщЊЁћв“вµ√![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ
Љі„‘––≥µґ”≥цЈҐЇу![]() –° ±їт
–° ±їт![]() –° ±”л„‘––≥µґ”ѕа”ц£Ѓ
–° ±”л„‘––≥µґ”ѕа”ц£Ѓ
£®3£©…ијлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋ![]() –° ±”л„‘––≥µґ”ѕаЊа
–° ±”л„‘––≥µґ”ѕаЊа![]() £Ѓ
£Ѓ
Ґўµ±![]() £ђҐўµ±„‘––≥µґ”‘Џƒ¶Ќ–≥µ«∞√ж ±£ђ
£ђҐўµ±„‘––≥µґ”‘Џƒ¶Ќ–≥µ«∞√ж ±£ђ![]()
љвµ√![]() £ї
£ї
ҐЏµ±ƒ¶Ќ–≥µ‘Џ„‘––≥µґ”«∞√ж ±£ђ![]() £ђ
£ђ
љвµ√![]() £ї
£ї
µ±![]() ±£ђҐўƒ¶Ќ–≥µі”““µЎЈµїЎ£ђ”л„‘––≥µґ”ќіѕа”ц£ђ
±£ђҐўƒ¶Ќ–≥µі”““µЎЈµїЎ£ђ”л„‘––≥µґ”ќіѕа”ц£ђ
![]() £ђљвµ√
£ђљвµ√![]() £ї
£ї
ҐЏƒ¶Ќ–≥µі”““µЎЈµїЎ£ђ”л„‘––≥µґ”ѕа”цЇу£ђ![]() £Ѓ
£Ѓ
љвµ√![]() £Ѓ
£Ѓ
Љіƒ¶Ќ–≥µ”л„‘––≥µґ”ѕаЊа![]() ±£ђіЋ ±јлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋ
±£ђіЋ ±јлƒ¶Ќ–≥µ≥цЈҐЊ≠єэЅЋ![]() –° ±їт
–° ±їт![]() –° ±їт
–° ±їт![]() –° ±їт
–° ±їт![]() –° ±£Ѓ
–° ±£Ѓ

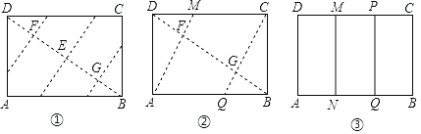
°Њћвƒњ°њ»зЌЉ£ђ“—÷™ЊЎ–ќ÷љ∆ђABCD£ђ‘х—щ’џµю£ђƒ№ є±яAB±ї»эµ»Ј÷£њ
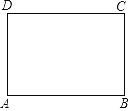
“‘ѕ¬ «–°Їмµƒ—–Њњєэ≥ћ£Ѓ
ЋЉњЉєэ≥ћ | “™ є±яAB±ї»эµ»Ј÷£ђ»фі”±яDC…ѕњЉ¬«£ђЊЌ «“™’џ≥цDM£љ “≤ЊЌ «“™’џ≥цDM£љ µ±DB°ҐAMѕаљї”ЏF ±£ђЉі“™’џ≥цґ‘љ«ѕя…ѕµƒDF£љ |
’џµюЈљЈ®ЇЌ Њ“вЌЉ | Ґў’џ≥цDB£їґ‘’џ÷љ∆ђ£ђ єD°ҐB÷ЎЇѕ£ђµ√µљµƒ’џЇџ”лDBѕаљї”ЏµгE£їЉћ–ш’џµю÷љ∆ђ£ђ єD°ҐB”лE÷ЎЇѕ£ђµ√µљµƒ’џЇџ”лDBЈ÷±рѕаљї”ЏµгF°ҐG£ї ҐЏ’џ≥цAF°ҐCG£ђЈ÷±рљї±яCD°ҐAB”ЏM°ҐQ£ї ҐџєэM’џ÷љ∆ђ£ђ єD¬д‘ЏMC…ѕ£ђµ√µљ’џЇџMN£ђ‘т±яAB±їN°ҐQ»эµ»Ј÷£Ѓ
|
£®1£©’ыјн–°Їмµƒ—–Њњєэ≥ћ£ђЋµ√чAN£љNQ£љQB£ї
£®2£©”√“ї÷÷”л–°Їм≤їЌђµƒЈљЈ®’џµю£ђ є±яAB±ї»эµ»Ј÷£Ѓ£®–иЉт ц’џµюЈљЈ®≤Ґї≠≥ц Њ“вЌЉ£©