题目内容
6．已知，四边形ABCD，AD平行于BC，AD≠BC，AB=DC，求证：A，B，C，D四点在同一圆上．分析 由等腰梯形的性质得出∠B=∠C，∠A+∠C=180°，即可得出A，B，C，D四点在同一圆上．
解答 证明：如图所示：
∵AD∥BC，AD≠BC，AB=DC，
∴∠A+∠B=180°，四边形ABCD是等腰梯形，
∴∠B=∠C，
∴∠A+∠C=180°，
∴A，B，C，D四点在同一圆上．
点评 本题考查了等腰梯形的性质、四点共圆；熟练掌握等腰梯形的性质，由等腰梯形的性质得出对角互补是解决问题的关键．
练习册系列答案
相关题目
16．某商品连续两次降价．单价由100元降至81元，若两次的降价的百分率一样，则这样百分率为（ ）
| A． | 10% | B． | 20% | C． | 30% | D． | 40% |
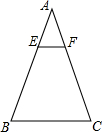如图，在△ABC中，E、F分别是AB、AC上的点，EF∥BC，且$\frac{AE}{EB}$=$\frac{1}{2}$，若△AEF的面积为2，则四边形EBCF的面积为（ ）