题目内容
试利用多项式运算说明下列结论是正确的:
(1)一个两位数,如果两个数字的和能被9整除,那么这个两位数也能被9整除.
(2)一个四位数,如果它的前位与十位上的数字之和减去百位与个位上的数字之和所得差能被11整除,那么这个四位数也能被11整除.
(1)一个两位数,如果两个数字的和能被9整除,那么这个两位数也能被9整除.
(2)一个四位数,如果它的前位与十位上的数字之和减去百位与个位上的数字之和所得差能被11整除,那么这个四位数也能被11整除.
考点:整式的加减
专题:
分析:(1)设出这个两位数为xy,根据题意列出代数式,进一步整理得出结论即可;
(2)设出这个四位数为abcd,根据题意列出代数式,进一步整理得出结论即可.
(2)设出这个四位数为abcd,根据题意列出代数式,进一步整理得出结论即可.
解答:解:(1)设两数为xy,由题意知x+y=9a(a为整数),
则xy=10x+y=9x+(x+y)=9a+9x=9(a+x)
所以这个两位数也能被9整除.
(2)设这个四位数为abcd,由题意得
(a+c)-(b+d)=11x(x为整数)
则abcd=1000a+100b+10c+d
=1001a+11c-(a+c)+99b+b+d
=1001a+11c+99b-[(a+c)-(b+d)]
=11(91a+c+9b)-11x
所以这个四位数也能被11整除.
则xy=10x+y=9x+(x+y)=9a+9x=9(a+x)
所以这个两位数也能被9整除.
(2)设这个四位数为abcd,由题意得
(a+c)-(b+d)=11x(x为整数)
则abcd=1000a+100b+10c+d
=1001a+11c-(a+c)+99b+b+d
=1001a+11c+99b-[(a+c)-(b+d)]
=11(91a+c+9b)-11x
所以这个四位数也能被11整除.
点评:此题考查整式的加减,掌握数的表示方法是解决问题的关键.

练习册系列答案
相关题目
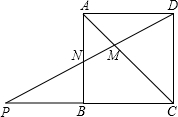 如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P,连接AC交DN于点M.若PN=3,则DM的长为
如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P,连接AC交DN于点M.若PN=3,则DM的长为