题目内容
4.计算:|2-$\sqrt{2}$|-8${\;}^{\frac{1}{3}}$+2-2+$\frac{1}{\sqrt{2}-1}$.分析 首先计算乘方,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:|2-$\sqrt{2}$|-8${\;}^{\frac{1}{3}}$+2-2+$\frac{1}{\sqrt{2}-1}$
=2-$\sqrt{2}$-2+$\frac{1}{4}$+$\sqrt{2}$+1
=1$\frac{1}{4}$
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
 如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )| A. | 32 | B. | 36 | C. | 40 | D. | 56 |
15.下列命题是真命题的是( )
| A. | 同旁内角互补 | B. | 相等的角是对顶角 | ||
| C. | 在同一平面内,如果a∥b,b∥c,则a∥c | D. | 在同一平面内,如果a⊥b,b⊥c,则a⊥c |
19.把多项式m2-9m分解因式,结果正确的是( )
| A. | m(m-9) | B. | (m+3)(m-3) | C. | m(m+3)(m-3) | D. | (m-3)2 |
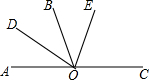 如图,O为直线AC上一点,OD是∠AOB的平分线,OE在∠BOC的内部,∠BOE=36°,∠EOC=$\frac{2}{3}$∠BOC.求∠AOD的度数.
如图,O为直线AC上一点,OD是∠AOB的平分线,OE在∠BOC的内部,∠BOE=36°,∠EOC=$\frac{2}{3}$∠BOC.求∠AOD的度数.
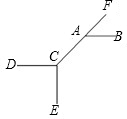 如图,∠FAB=46°,CE⊥CD,当∠FCE=136°时,CD∥AB.
如图,∠FAB=46°,CE⊥CD,当∠FCE=136°时,CD∥AB.