��Ŀ����
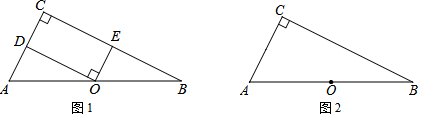
5����Rt��ABC�У���ACB=90�㣬OΪAB���ϵ�һ�㣬��tanB=$\frac{1}{2}$����DΪAC���ϵĶ��㣨�����A��C�غϣ������߶�OD�Ƶ�O˳ʱ����ת90�㣬��BC�ڵ�E����1����ͼ1����OΪAB���е㣬DΪAC���е㣬��$\frac{OE}{OD}$��ֵΪ$\frac{1}{2}$��
��2����OΪAB���е㣬D����AC�ߵ��е㣬
����������⽫ͼ2��ȫ��
��С��ͨ���۲졢ʵ�飬������룺��D��AC�����˶��Ĺ����У���1����$\frac{OE}{OD}$��ֵ���䣮С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ�����$\frac{OE}{OD}$��ֵ�ļ����뷨��
�뷨1������O��OF��AB��BC�ڵ�F��Ҫ��$\frac{OE}{OD}$��ֵ����֤����OEF�ס�ODA��
�뷨2���ֱ�ȡAC��BC���е�H��G������OH��OG��Ҫ��$\frac{OE}{OD}$��ֵ����֤����OGE�ס�OHD��
�뷨3������OC��DE��Ҫ��$\frac{OE}{OD}$��ֵ����֤C��D��O��E�ĵ㹲Բ��
��
����ο�������뷨������С��д����$\frac{OE}{OD}$��ֵ�Ĺ���?��һ�ַ������ɣ���
��3����$\frac{BO}{BA}$=$\frac{1}{n}$��n��2��nΪ������������$\frac{OE}{OD}$��ֵΪ$\frac{1}{2n-2}$���ú�n��ʽ�ӱ�ʾ����
���� ��1������OΪAB���е㣬DΪAC���е㣬�ó��ı���CDOE�Ǿ��Σ��ٸ���tanB=$\frac{1}{2}$=tan��AOD���ó�$\frac{AD}{OD}$=$\frac{1}{2}$�������õ�$\frac{OE}{OD}$=$\frac{1}{2}$��
��2���ٸ������⽫ͼ2��ȫ���ɣ��ڷ�1������O��OF��AB��BC�ڵ�F��Ҫ��$\frac{OE}{OD}$��ֵ����֤����OEF�ס�ODA����2���ֱ�ȡAC��BC���е�H��G������OH��OG��Ҫ��$\frac{OE}{OD}$��ֵ����֤����OGE�ס�OHD����3������OC��DE��Ҫ��$\frac{OE}{OD}$��ֵ����֤C��D��O��E�ĵ㹲Բ���ֱ�������ַ������н�ɣ�
��3���ȹ���O��OF��AB��BC�ڵ�F��Ҫ��$\frac{OE}{OD}$��ֵ����֤����OEF�ס�ODA���ó�$\frac{OE}{OD}=\frac{OF}{OA}$���ٸ���$\frac{BO}{BA}$=$\frac{1}{n}$��n��2��nΪ�����������õ�$\frac{OF}{OA}$=$\frac{1}{2n-2}$���ɣ�
��� �⣺��1����ͼ1����OΪAB���е㣬DΪAC���е㣬
��OD��BC����CDO=90�㣬
�֡ߡ�ACB=90�㣬��DOE=90�㣬
���ı���CDOE�Ǿ��Σ�
��OE=CD=AD��
��OD��BC��
���AOD=��B��
��tanB=$\frac{1}{2}$=tan��AOD����$\frac{AD}{OD}$=$\frac{1}{2}$��
��$\frac{OE}{OD}$=$\frac{1}{2}$��
�ʴ�Ϊ��$\frac{1}{2}$��
��2������ͼ��ʾ��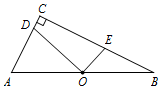
�ڷ�1����ͼ������O��OF��AB��BC�ڵ�F��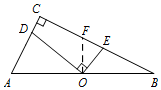
�ߡ�DOE=90�㣬
���AOD+��DOF=��DOF+��FOE=90�㣬
���AOD=��FOE��
�ߡ�ACB=90�㣬
���A+��B=��OFE+��B=90�㣬
���A=��OFE��
���OEF�ס�ODA��
��$\frac{OE}{OD}=\frac{OF}{OA}$��
��OΪAB���е㣬
��OA=OB��
��Rt��FOB��tanB=$\frac{1}{2}$��
��$\frac{OF}{OB}=\frac{1}{2}$��
��$\frac{OF}{OA}=\frac{1}{2}$��
��$\frac{OE}{OD}=\frac{1}{2}$��
��2����ͼ���ֱ�ȡAC��BC���е�H��G������OH��OG��
��OΪAB���е㣬
��OH��BC��OH=$\frac{1}{2}BC$��OG��AC��
�ߡ�ACB=90�㣬
���OHD=��OGE=90�㣬
���HOG=90�㣬
�ߡ�DOE=90�㣬
���HOD+��DOG=��DOG+��GOE=90�㣬
���HOD=��GOE��
���OGE�ס�OHD��
��$\frac{OE}{OD}=\frac{OG}{OH}$��
��tanB=$\frac{1}{2}$��
��$\frac{OG}{GB}=\frac{1}{2}$��
��OH=GB��
��$\frac{OG}{OH}=\frac{1}{2}$��
��$\frac{OE}{OD}=\frac{1}{2}$��
��3����ͼ������OC��DE��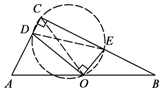
�ߡ�ACB=90�㣬��DOE=90�㣬
��DE���е㵽��C��D��O��E�ľ�����ȣ�
��C��D��O��E�ĵ㹲Բ��
���ODE=��OCE��
��OΪAB���е㣬
��OC=OB��
���B=��OCE��
���ODE=��B��
��tanB=$\frac{1}{2}$��
��$\frac{OE}{OD}=\frac{1}{2}$��
��3����ͼ��ʾ������O��OF��AB��BC�ڵ�F��
�ߡ�DOE=90�㣬
���AOD+��DOF=��DOF+��FOE=90�㣬
���AOD=��FOE��
�ߡ�ACB=90�㣬
���A+��B=��OFE+��B=90�㣬
���A=��OFE��
���OEF�ס�ODA��
��$\frac{OE}{OD}=\frac{OF}{OA}$��
��$\frac{BO}{BA}$=$\frac{1}{n}$��
�����OB=1����AB=n��AO=n-1��
����Rt��FOB��tanB=$\frac{1}{2}$��
��OF=$\frac{1}{2}$��
��$\frac{OF}{OA}$=$\frac{\frac{1}{2}}{n-1}$=$\frac{1}{2n-2}$��
��$\frac{OE}{OD}$=$\frac{1}{2n-2}$��
�ʴ�Ϊ��$\frac{1}{2n-2}$��
���� ���������������ۺ��⣬��Ҫ���������������ε��ж������ʵ��ۺ�Ӧ�ã�Ѱ�����������ε�һ�㷽����ͨ����ƽ���߹������������Σ������ݻ���ͼ�ζ�ͼ�ν��зֽ⡢��ϣ����������߹������������Σ��ж����������Ƶķ�����ʱ�ɵ���ʹ�ã���ʱ��Ҫ�ۺ����ã�

 53���ò�ϵ�д�
53���ò�ϵ�д�| A�� | 2 | B�� | 1 | C�� | -2 | D�� | -3 |
| x | �� | -2 | -1 | 0 | 2 | �� |
| y | �� | -3 | -4 | -3 | 5 | �� |
��2������ú���ͼ����x��Ľ������꣮
| A�� | m6��m2=m3 | B�� | 3m3-2m2=m | C�� | ��3m2��3=27m6 | D�� | $\frac{1}{2}$m•2m2=m2 |
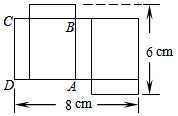 ��ͼ��һ��������ı���չ��ͼ���ı���ABCD�������Σ������ͼ�����ݿɵ�ԭ������������12cm3��
��ͼ��һ��������ı���չ��ͼ���ı���ABCD�������Σ������ͼ�����ݿɵ�ԭ������������12cm3��
 ������a��b��c�������ϵ�λ����ͼ��ʾ������|a+c|-|a-b|+|b+c|-|b|��
������a��b��c�������ϵ�λ����ͼ��ʾ������|a+c|-|a-b|+|b+c|-|b|��