Question

12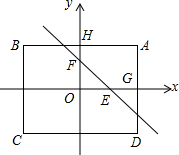．如图，已知矩形ABCD的面积为48，以此矩形的对称轴为坐标轴建立直角坐标系．设A（x，y），其中x＞0，y＞0．
（1）求y关于x的函数关系式及自变量x的取值范围；
（2）若一次函数y=mx+2（m＜0）的图象与x轴y轴分别交点于点E、F，设A（4，3），那么是否存在实数m，使得△AFE的面积是矩形ABCD面积的$\frac{1}{8}$？若存在，请求出m值；若不存在，请说明理由．

Answer 1

分析 （1）由点A的坐标结合矩形ABCD的面积为48，即可得出4xy=48，将其变形后即可得出结论；
（2）假设存在，由一次函数的解析式可得出点E、F的坐标，通过分割图形求面积法结合△AFE的面积是矩形ABCD面积的$\frac{1}{8}$，即可得出关于m的方程，解方程即可得出结论．

解答 解：（1）∵矩形ABCD的面积为48，A（x，y），
∴4xy=48，
∴y=$\frac{12}{x}$（x＞0）．
（2）假设存在．
当x=0时，y=2，
∴F（0，2）；
当y=0时，有0=mx+2，
解得：x=-$\frac{2}{m}$，
∴E（-$\frac{2}{m}$，0）．
∴S_△AEF=S_矩形AHOG-S_△AHF-S_△OEF-S_△AEG=3×4-$\frac{1}{2}$×（3-2）×4-$\frac{1}{2}$×2×（-$\frac{2}{m}$）-$\frac{1}{2}$×3×（4+$\frac{2}{m}$）=$\frac{1}{8}$×48，
即4-$\frac{1}{m}$=6，
解得：m=-$\frac{1}{2}$，
经检验m=-$\frac{1}{2}$是分式方程4-$\frac{1}{m}$=6的解．
故存在实数m=-$\frac{1}{2}$，使得△AFE的面积是矩形ABCD面积的$\frac{1}{8}$．

点评 本题考查了一次函数图象上点的坐标特征、矩形的性质以及三角形的面积，解题的关键是：（1）根据矩形的面积为48找出x、y之间的关系；（2）找出关于m的方程．本题属于中档题，难度不大，解决该题型题目时，利用分割图形法求出三角形的面积是关键．