题目内容
6.半径为10cm的圆内接正六边形的面积为150$\sqrt{3}$cm2.分析 设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形,△OAB的面积的六倍就是正六边形的面积.
解答 解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,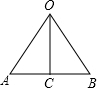
∠AOB=60°,OA=OB=10cm,
则△OAB是正三角形,
∵OC=OA•sin∠A=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$(cm),
∴S△OAB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×10×5$\sqrt{3}$=25$\sqrt{3}$(cm2),
∴正六边形的面积为25$\sqrt{3}×6$=150$\sqrt{3}$(cm2).
故答案为:150$\sqrt{3}$cm2.
点评 本题考查的正多边形和圆,理解正六边形被半径分成六个全等的等边三角形是解答此题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
16.为迎接建国六十周年,园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配成A、B两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉请况如下表所示:
结合上述信息,解答下列问题:
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1200元,试说明(1)中哪种方案成本最低,最低成本是多少?
| 造型 | 甲 | 乙 |
| A | 90 | 30 |
| B | 40 | 100 |
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1200元,试说明(1)中哪种方案成本最低,最低成本是多少?
17.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等边三角形 | D. | 直角三角形 |
1.66路公交车沿东西方向行驶,如果把车站的起点记为0,向东行驶记为正,向西行驶记为负,其中一辆车从车站出发以后行驶的路程(单位:km)依次如下表所示:
(1)该车最后是否回到了车站?为什么?
(2)这辆车离开出发点最远是多少千米?用数轴表示.
(3)这辆车在上述过程中一共行驶了多少千米?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
(2)这辆车离开出发点最远是多少千米?用数轴表示.
(3)这辆车在上述过程中一共行驶了多少千米?
15.如果$\sqrt{2}$是a-1的相反数,那么a的值是( )
| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
16.分式$\frac{{a}^{2}+a}{{a}^{2}+2a+1}$化简的结果是( )
| A. | $\frac{a}{a-1}$ | B. | $\frac{a+1}{a-1}$ | C. | $\frac{a}{a+1}$ | D. | a |