题目内容
9.菱形的一个内角为120°,且平分这个内角的对角线长为8cm,则这个菱形的面积为$32\sqrt{3}$cm2.分析 根据已知可得该对角线与菱形的一组邻边构成一个等边三角形,从而可求得菱形的边长,根据勾股定理得出另一条对角线求出面积即可.
解答 解:菱形的一个内角为120°,则邻角为60°
则这条对角线和一组邻边组成等边三角形,
可得边长为8cm,
另一条对角线为:2×$\sqrt{{8}^{2}-{4}^{2}}=8\sqrt{3}$,
这个菱形的面积为:$\frac{1}{2}×8×8\sqrt{3}=32\sqrt{3}$cm2.
故答案为:$32\sqrt{3}$cm2.
点评 此题主要考查菱形的性质和等边三角形的判定的运用,难度不大,关键熟练掌握菱形的性质.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
19.如果a的倒数是-2,那么a等于( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
4. 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )| A. | 150° | B. | 80° | C. | 100° | D. | 115° |
1.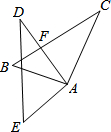 如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )
如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )
 如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )
如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )| A. | 84° | B. | 80° | C. | 60° | D. | 90° |
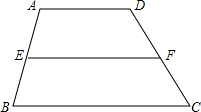 (1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;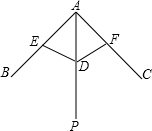 我国纸伞的制作工艺十分巧妙.如图,伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,且AE=AF,DE=DF,从而保证伞圈能沿着伞柄滑动.有一种玩具伞张开时,BDC在同一直线上,若AB=50cm,AD=14cm,则制作一把这样的纸伞需要油纸的面积是(不记接缝)( )
我国纸伞的制作工艺十分巧妙.如图,伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,且AE=AF,DE=DF,从而保证伞圈能沿着伞柄滑动.有一种玩具伞张开时,BDC在同一直线上,若AB=50cm,AD=14cm,则制作一把这样的纸伞需要油纸的面积是(不记接缝)( )