题目内容
20.对x,y定义一种新运算T,规定:T(x,y)=$\frac{ax+by}{2x+y}$(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=$\frac{a×0+b×1}{2×0+1}$=b.已知T(1,-1)=-2,T(4,2)=1.(1)求a,b的值;
(2)若T(m,m+3)=-1,求m的值.
分析 (1)已知等式利用题中的新定义化简,得到方程组,求出方程组的解即可得到a与b的值;
(2)已知等式利用题中的新定义化简,求出解即可得到m的值.
解答 解:(1)根据题中的新定义得:T(1,-1)=$\frac{a-b}{2-1}$=a-b=-2①,
T(4,2)=$\frac{4a+2b}{8+2}$=1,即2a+b=5②,
①+②得:3a=3,即a=1,
把a=1代入①得:b=3;
(2)根据题中的新定义得:T(m,m+3)=$\frac{m+3m+9}{2m+m+3}$=$\frac{4m+9}{3m+3}$=-1,
解得:m=-$\frac{12}{7}$,
经检验m=-$\frac{12}{7}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
8.下列计算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (ab2)2=ab4 | C. | 2a+3a=5a2 | D. | 2a•3a2=6a3 |
12.下列各题中是无理数的是( )
| A. | $\sqrt{9}$ | B. | $\frac{π}{2}$ | C. | $\frac{24}{7}$ | D. | $\root{3}{8}$ |
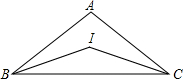 如图,△ABC中,AB=AC,∠ABC=40°,点I是△ABC的内心,则∠BAC的度数为100°.
如图,△ABC中,AB=AC,∠ABC=40°,点I是△ABC的内心,则∠BAC的度数为100°.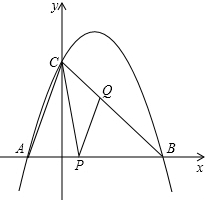 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.