题目内容
2.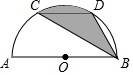 如图,AB是半圆的直径,C、D是$\widehat{AB}$的三分之一点,若半径为R,求阴影部分的面积.
如图,AB是半圆的直径,C、D是$\widehat{AB}$的三分之一点,若半径为R,求阴影部分的面积.
分析 首先连OC、OD,根据弧相等则弧所对的圆心角相等得到∠AOC=∠COD=∠BOD=$\frac{1}{3}$×180°=60°,则△OCD为等边三角形,即有∠OCD=60°,所以CD∥AB,于是得到S△ECD=S△OCD,可把求阴影部分的面积的问题转化为求扇形OCD的面积,然后根据扇形的面积公式计算即可.
解答 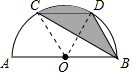 解:如图,连接OC、OD.
解:如图,连接OC、OD.
∵AB为半圆的直径,点C、D三等分半圆
∴∠AOC=∠COD=∠BOD=$\frac{1}{3}$×180°=60°,
而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△BCD=S△OCD,
∴S阴影=S扇形OCD=$\frac{60π×{R}^{2}}{360}$=$\frac{π{R}^{2}}{6}$.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$(n为扇形的圆心角的度数,R为圆的半径)以及弧与圆心角之间的关系以及等边三角形的性质,根据已知得出阴影部分的面积=S扇形OCD是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
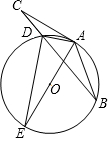 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.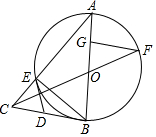 如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.
如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.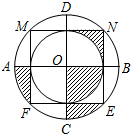 如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.
如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.