题目内容
19.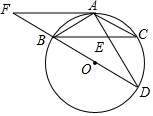 如图,BD为⊙O的直径,AD交BC于点E,AE=2,ED=4,过点A作⊙O的切线FA交DB延长线于点F,且AF∥BC.
如图,BD为⊙O的直径,AD交BC于点E,AE=2,ED=4,过点A作⊙O的切线FA交DB延长线于点F,且AF∥BC.(1)求证:AB=AC;
(2)求AF的长.
分析 (1)连接OA,由AF是⊙O的切线知OA⊥AF,根据AF∥BC即可得OA⊥BC,从而根据垂径定理得证;
(2)先根据相似三角形的判定得到△ABE∽△ADB,从而根据相似三角形的对应边成比例即可得到AB的长,根据圆周角定理求得△ABD是直角三角形,根据正切函数求得∠D=30°,求得∠AOB=60°,证得OA=OB=AB=2$\sqrt{3}$,在Rt△AOF中,通过正切函数即可求得AF的长.
解答 解:(1)如图,连接OA,
∵AF是⊙O的切线,
∴OA⊥AF,
∵AF∥BC,
∴OA⊥BC,
∴AB=AC;
(2)∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴∠ABE=∠ADB,
∵∠BAE=∠DAB=90°,∠ABE=∠ADB,
∴△ABE∽△ADB.
∴$\frac{AB}{AD}$=$\frac{AE}{AB}$.
∴AB2=AE•AD=2×(2+4)=12.
∴AB=2$\sqrt{3}$,
∵BD为⊙O的直径,
∴∠BAD=90°,
∵tan∠D=$\frac{AB}{AD}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠D=30°,
∴∠AOB=60°,
∴OA=OB=AB=2$\sqrt{3}$,
∵OA⊥AF,
∴tan∠AOF=$\frac{AF}{OA}$=$\sqrt{3}$,
∴AF=$\sqrt{3}$OA=$\sqrt{3}$×$2\sqrt{3}$=6.
点评 此题主要考查切线的判定,平行线的性质,圆周角定理以及正切函数等知识点的综合运用,熟练掌握性质定理是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
8. 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n,2n-1) | C. | (2n-1,2n+1) | D. | (2n-1,2n) |
9.分解因式4x4-64的结果为( )
| A. | 4(x4-16) | B. | (2x2+8)(2x2-8) | C. | 4(x2+4)(x2-4) | D. | 4(x2+4)(x+2)(x-2) |
 如图,在半圆AOB中,半径OA=2,C、D两点在半圆上,若四边形OACD为菱形,则图中阴影部分的面积是2π-2$\sqrt{3}$.
如图,在半圆AOB中,半径OA=2,C、D两点在半圆上,若四边形OACD为菱形,则图中阴影部分的面积是2π-2$\sqrt{3}$.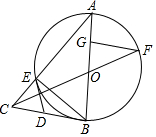 如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.
如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G. 在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).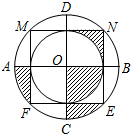 如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.
如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.