题目内容
18．在Rt△ABC中，∠BAC=90°，AB=3，BC=5，若将Rt△ABC绕直线BC旋转一周，则所得立体图形的侧面积为 （ ）| A． | 6π | B． | 9π | C． | 15π | D． | $\frac{84}{5}$π |
分析 根据勾股定理易得AC的长，利用直角三角形的面积求得AB边上的高，根据几何体为两个圆锥的组合体，表面积为底面半径为2.4，母线长为3，4的两个圆锥的侧面积的和计算即可．
解答 解：∵∠BAC=90°，AB=3，BC=5，
由勾股定理得，AC=4，
∴AB边上的高为3×4÷5=2.4，
∴所得几何体的表面积是$\frac{1}{2}$×2π×2.4×3+$\frac{1}{2}$×2π×2.4×4=16.8π．
故选：D．
点评 本题考查了圆锥的计算；得到几何体的组成是解决本题的突破点，注意圆锥的侧面积=π×底面半径×母线长．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
已知△ABC，尺规作图．求作：
如图，AD∥BF，BE∥CG，∠DAB=45°，∠BCG=110°，求∠EBF的度数．
3．
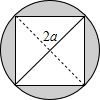如图，直径为2a的圆中有一个正方形，那么阴影部分的面积为（ ）
如图，直径为2a的圆中有一个正方形，那么阴影部分的面积为（ ）| A． | （4-π）a2 | B． | （π-3）a2 | C． | （π-2.5）a2 | D． | （π-2）a2 |
如图，在等边△ABC中，点D、E分别是AB、BC的中点，AD=6，点P是AD上的一动点，则PE+PB的最小值为6．
有理数a，b，c在数轴上的位置如图所示，化简：$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$．