题目内容
19.抛物线y=-x2+mx-4的对称轴是直线x=3,则m=6.分析 根据抛物线的对称轴为直线x=3,即可得出$\frac{m}{2}$=3,解之即可得出m的值.
解答 解:∵抛物线y=-x2+mx-4的对称轴是直线x=3,
∴-$\frac{m}{2×(-1)}$=$\frac{m}{2}$=3,
解得:m=6.
故答案为:6.
点评 本题考查了二次函数的性质,牢记“二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=-$\frac{b}{2a}$”是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.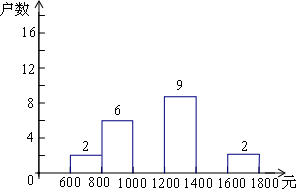 小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)频数分布表中:a=16,b=5,c=12.5%.
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
 小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.| 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | a | 40% |
| 1200≤x<1400 | 9 | 22.5% |
| 1400≤x<1600 | b | c |
| 1600≤x<1800 | 2 | 5% |
| 合计 | 40 | 100% |
(1)频数分布表中:a=16,b=5,c=12.5%.
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
4.在-2,0,1,$\sqrt{2}$四个实数中属于无理数的是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 0 | D. | -2 |
7.如果M(x1,y1),N(x2,y2)是一次函数y=kx+2的图象上的两点,且x1+x2=-3,y1+y2=5,那么k的值为( )
| A. | 1 | B. | 2 | C. | -3 | D. | -$\frac{1}{3}$ |
8.已知关于x的二次函数y=-(x-h)2+3,当1≤x≤3时,函数有最小值h,则h的值为( )
| A. | -1或3 | B. | 2 | C. | 2或3 | D. | -1 |
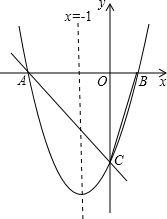 如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-3,0).
如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-3,0).