题目内容
如图，∠AOB和∠COD有公共顶点，OA⊥OC，OB⊥OD，∠AOB：∠COD=7：13，求∠AOB和∠COD的度数．考点：垂线
专题：
分析：根据圆周角等于360°先求出∠AOB+∠COD等于180°，再根据∠AOB：∠COD=7：13即可求出两角的度数．
解答：解：∵OA⊥OC，OB⊥OD
∠AOC=∠BOD=90°，
∴∠AOB+∠COD=360°-90°-90°=180°，
∵AOB：∠COD=7：13
∴∠AOB=180°×
=63°，∠COD=180°×
=117°，
故∠AOB和∠COD的度数分别为63°，117°．
∠AOC=∠BOD=90°，
∴∠AOB+∠COD=360°-90°-90°=180°，
∵AOB：∠COD=7：13
∴∠AOB=180°×
| 7 |
| 7+13 |
| 13 |
| 7+13 |
故∠AOB和∠COD的度数分别为63°，117°．
点评：本题考查了垂线，根据圆周角等于360°求出∠AOB+∠COD等于180°是解本题的关键．
练习册系列答案
相关题目
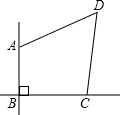农民牛伯伯承包了一块四边形水稻田ABCD如图，他量得边长AB=90m，BC=120m，CD=130m，DA=140m，且边AB，BC正好位于两条相互垂直的公路的拐角处，请你帮牛伯伯计算一下这块水稻田的面积．
已知等腰△ABC中，AB=AC=13，BC=10，求顶角∠A的正弦值．
如图所示，OB=1，OC=3，AB=AC=4，求点A的坐标．
如图所示，在△ABC中，∠ACB=90°，∠ADC=∠ACD，∠BCE=∠BEC，求∠DCE的度数．
如图，∠1，∠2，∠3，∠4，∠5，∠6中有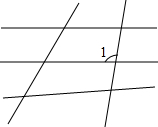
在图中，先标上适当的字母，再回答下列问题；
如图，△ABD是等腰直角三角形，∠BAD=90°，BC∥AD，BC=2AB，CE平分∠BCD，交AB于E，交BD于H．求证：