题目内容
 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 4 |
| 3 |
考点:翻折变换(折叠问题)
专题:
分析:如图,证明BE=DE,此为解题的关键;运用勾股定理求出DE,即可解决问题.
解答: 解:如图,∵四边形ABCD是矩形,
解:如图,∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=3;AD∥BC;
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC;而∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴BE=DE(设为λ),则AE=3-λ;
由勾股定理得:λ2=(
)2+(3-λ)2,
解得:λ=
,
∴阴影部分的面积=
DE•AB=
×
×
=
.
故答案为
.
 解:如图,∵四边形ABCD是矩形,
解:如图,∵四边形ABCD是矩形,∴∠A=90°,AD=BC=3;AD∥BC;
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC;而∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴BE=DE(设为λ),则AE=3-λ;
由勾股定理得:λ2=(
| 4 |
| 3 |
解得:λ=
| 97 |
| 54 |
∴阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 97 |
| 54 |
| 4 |
| 3 |
| 97 |
| 81 |
故答案为
| 97 |
| 81 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用勾股定理等几何知识点来分析、判断.

练习册系列答案
相关题目
在Rt△ABC中,∠C=Rt∠,若∠A=30°,则cosA+sinB等于( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知OC是∠AOB的平分线,则下列结论不正确的是( )
| A、∠AOC=∠BOC | ||
B、∠AOC=
| ||
| C、∠AOB=2∠BOC | ||
| D、∠AOB=∠BOC |
已知圆的半径是R,则圆内接正十边形的边长是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,
如图所示,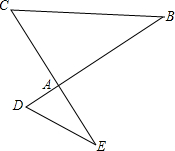 如图,BD、CE相交于点A.
如图,BD、CE相交于点A. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.