题目内容
4.给出下列函数:①y=2x-1;②y=$\frac{1}{x}$;③y=-2x2.从中任取一个函数,取出的函数符合条件“当x>1时,函数值y随x增大而减小”的概率是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 0 |
分析 首先利用一次函数、反比例函数及二次函数的性质确定当x>1时,函数值y随x增大而减小的个数,然后利用概率公式求解即可.
解答 解:∵函:①y=2x-1;②y=$\frac{1}{x}$;③y=-2x2中当x>1时,函数值y随x增大而减小的有y=$\frac{1}{x}$、y=-2x2,
∴从中任取一个函数,取出的函数符合条件“当x>1时,函数值y随x增大而减小”的概率是$\frac{2}{3}$.
故选C.
点评 本题考查的是用列举法求概率的知识.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
14.下列运算中,正确的是( )
| A. | (-a2b3)2=a4b6 | B. | (-2a)2=-4a2 | C. | (a+b)2=a2+b2 | D. | b2•b3=2b3 |
15.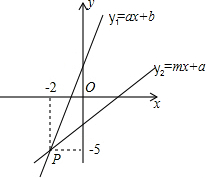 如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )
如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )
 如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )
如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )| A. | x>-5 | B. | x>-2 | C. | x<-2 | D. | x<-5 |
16.为了促进湖北省的经济发展,省政府提出了总计约为1.2万亿元的投资计划,将1.2万亿用科学记数法表示应为( )
| A. | 1.2×1010 | B. | 1.2×1011 | C. | 1.2×1012 | D. | 1.2×1013 |
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2,AB=16cm,AC=14cm,则DE=3.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2,AB=16cm,AC=14cm,则DE=3.