Question

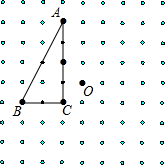在下列方形点阵中有直角△ABC和点O，将△ABC以O为旋转中心逆时针分别旋转
90°，180°，270°，
（1）请画出旋转后的图形；
（2）求点B在整个旋转过程中所经过的路径；
（3）求线段AC在整个旋转过程中所扫过的面积．

Answer 1

考点：作图-旋转变换,弧长的计算,扇形面积的计算

专题：作图题

分析：（1）画出旋转后的图形，如图1所示；
（2）B在整个旋转过程中所经过的路径为半径为

10

，圆周角为270度的弧长，求出即可；
（3）线段AC在整个旋转过程中所扫过的面积为半径为

10

与半径为1的圆环面积的

2

3

，求出即可．

解答：解：（1）如图1所示；

（2）如图2所示，弧所在圆的半径为

32+12

=

10

，
则B在整个旋转过程中所经过的路径为

270π× 10

180

=

3 10 π

2

；

（3）如图3所示，线段AC在整个旋转过程中所扫过的面积S=

2

3

×（π×（

10

）²-π×1²）=6π．

点评：此题考查了作图-旋转变换，弧长公式，以及扇形的面积求法，熟练掌握公式是解本题的关键．