题目内容
 如图,E是正方形ABCD边CD的中点,AE与BD交于点O,则tan∠AOB=
如图,E是正方形ABCD边CD的中点,AE与BD交于点O,则tan∠AOB=考点:相似三角形的判定与性质,勾股定理,正方形的性质,锐角三角函数的定义
专题:
分析:连接AC交BD于F,设正方形的边长为2,则DE=1,由正方形的性质可知:DE∥AB,所以△EOD∽△AOB,根据勾股定理可求出AE和BD的长,由相似三角形的性质可得AO和OE的比值,进而求出AO,根据正方形的对角线互相平分可求出AF,进而求出tan∠AOB的值.
解答: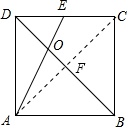 解:连接AC交BD于F,设正方形的边长为2,
解:连接AC交BD于F,设正方形的边长为2,
∵E是正方形ABCD边CD的中点,
∴则DE=1,
∴AE=
=
,
∵四边形ABCD是正方形,
∴DE∥AB,AC⊥BD于F,
∴△EOD∽△AOB,
∴DE:AB=EO:AO=1:2,
∴AO=
,
∵AC=
=2
,
∴AF=
×2
=
,
∴OF=
=
,
∴tan∠AOB=
=
=3,
故答案为:3.
 解:连接AC交BD于F,设正方形的边长为2,
解:连接AC交BD于F,设正方形的边长为2,∵E是正方形ABCD边CD的中点,
∴则DE=1,
∴AE=
| 22+12 |
| 5 |
∵四边形ABCD是正方形,
∴DE∥AB,AC⊥BD于F,
∴△EOD∽△AOB,
∴DE:AB=EO:AO=1:2,
∴AO=
2
| ||
| 3 |
∵AC=
| 22+22 |
| 2 |
∴AF=
| 1 |
| 2 |
| 2 |
| 2 |
∴OF=
| AO2-AF2 |
| ||
| 3 |
∴tan∠AOB=
| AF |
| OF |
| ||||
|
故答案为:3.
点评:本题考查了正方形的性质、勾股定理的运用、相似三角形的判定和性质以及锐角三角函数的定义,题目的综合性很强,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算(
-1)(
+1)的结果是( )
| 2 |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
D、3+2
|
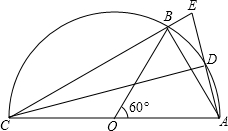 如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.
如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.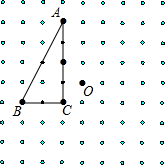 在下列方形点阵中有直角△ABC和点O,将△ABC以O为旋转中心逆时针分别旋转
在下列方形点阵中有直角△ABC和点O,将△ABC以O为旋转中心逆时针分别旋转 已知△ABC在平面直角坐标系xOy中的位置如图所示,△ABC绕点B顺时针旋转90°后得到△A′B′C′.
已知△ABC在平面直角坐标系xOy中的位置如图所示,△ABC绕点B顺时针旋转90°后得到△A′B′C′.