题目内容
18. 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )
如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定△ADG≌△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再抓住△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的.
解答 解:由折叠可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
∴△ADG≌△FDG,①正确;
∵正方形边长是12,
∴BE=EC=EF=6,
设AG=FG=x,则EG=x+6,BG=12-x,
由勾股定理得:EG2=BE2+BG2,
即:(x+6)2=62+(12-x)2,
解得:x=4
∴AG=GF=4,BG=8,BG=2AG,②正确;
BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,③错误;
S△GBE=$\frac{1}{2}$×6×8=24,S△BEF=$\frac{EF}{EG}$•S△GBE=$\frac{6}{10}•24$=$\frac{72}{5}$,④正确.
故选:C.
点评 本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算,有一定的难度.

练习册系列答案
相关题目
8.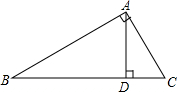 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )| A. | BC=$\frac{AC}{sinα}$ | B. | CD=AD•tanα | C. | BD=ABcosα | D. | AC=ADcosα |
13.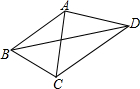 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )| A. | 68° | B. | 88° | C. | 90° | D. | 112° |
3.在数轴上表示不等式2(1-x)<4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
10.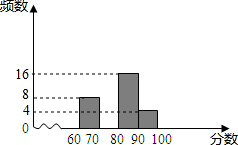 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
请根据图表提供的信息,解答下列问题:
(1)表中的a=12,b=40;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是108°;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为$\frac{2}{3}$.
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图| 分数段(分手为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x≤90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
(1)表中的a=12,b=40;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是108°;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为$\frac{2}{3}$.
7.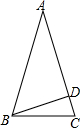 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )| A. | 36° | B. | 54° | C. | 18° | D. | 64° |
8.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
| A. | 4,4 | B. | 3,4 | C. | 4,3 | D. | 3,3 |
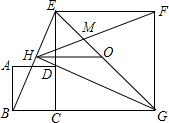 如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②HO$\stackrel{∥}{=}$$\frac{1}{2}$BG;③S正方形ABCD:S正方形ECGF=1:$\sqrt{2}$;④EM:MG=1:(1+$\sqrt{2}$),其中正确结论的序号为①②④.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②HO$\stackrel{∥}{=}$$\frac{1}{2}$BG;③S正方形ABCD:S正方形ECGF=1:$\sqrt{2}$;④EM:MG=1:(1+$\sqrt{2}$),其中正确结论的序号为①②④.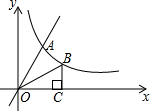 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.