题目内容
18. 反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A,已知AO=AB,S△OAB=4,则k的值为( )
反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A,已知AO=AB,S△OAB=4,则k的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 作AD⊥x轴于D,根据等腰三角形的性质得到OD=BD,则S△AOD=$\frac{1}{2}$S△ABD=$\frac{1}{2}$×4=2,然后根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义求解.
解答  解:作AD⊥x轴于D,如图,
解:作AD⊥x轴于D,如图,
∵AO=AB,
∴OD=BD,
∴S△ADO=$\frac{1}{2}$S△ABD=$\frac{1}{2}$×4=2,
∴$\frac{1}{2}$k=2,
∴k=4.
故选B.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.也考查了等腰三角形的性质.

练习册系列答案
相关题目
8.下列各数中,最小的数是( )
| A. | -0.5 | B. | 0 | C. | -2 | D. | 1 |
6.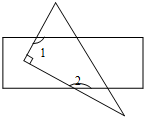 如图,将一张矩形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的值是( )
如图,将一张矩形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的值是( )
 如图,将一张矩形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的值是( )
如图,将一张矩形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的值是( )| A. | 180° | B. | 240° | C. | 270° | D. | 300° |
10. 图中几何体的主视图是( )
图中几何体的主视图是( )
 图中几何体的主视图是( )
图中几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
8.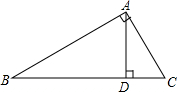 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )| A. | BC=$\frac{AC}{sinα}$ | B. | CD=AD•tanα | C. | BD=ABcosα | D. | AC=ADcosα |
